늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(6-3)]프로토타입과 크리티시즘(Prototypes and Criticisms) 본문
[해석할 수 있는 기계학습(6-3)]프로토타입과 크리티시즘(Prototypes and Criticisms)
Justin T. 2021. 3. 20. 17:37프로토타입(Prototype)은 모든 데이터를 대표하는 데이터 인스턴스입니다. 크리티시즘(Criticism)은 프로토타입 집합으로 잘 표현되지 않는 데이터 인스턴스입니다. 크리티시즘의 목적은 프로토타입과 함께 통찰력, 특히 프로토타입이 잘 표현하지 못하는 데이터 포인트에 대한 통찰력을 제공하는 것입니다. 프로토타입과 크리티시즘은 기계학습 모델과 독립적으로 데이터를 기술하는 데 사용될 수 있지만, 해석할 수 있는 모델을 만들거나 블랙박스 모델을 해석할 수 있는 모델로 만드는 데도 사용할 수 있습니다.
이번 포스팅에서는 하나의 인스턴스를 지칭하기 위해 "데이터 포인트"라는 표현을 사용하고, 한 인스턴스가 각 특성이 차원인 좌표계의 포인트라는 해석을 강조하고자 합니다. 아래의 그림은 시뮬레이션된 데이터 분포를 보여 주며, 일부 인스턴스는 프로토타입으로 선택되고 일부는 크리티시즘으로 선택되었습니다. 작은 점들은 데이터를, 큰 점은 크리티시짐을, 그리고 그보다 큰 정사각형은 프로토타입입니다. 프로토타입은 데이터 분포의 중심을 커버하기 위해 (수동적으로) 선택되며, 크리티시즘은 프로토타입이 없는 클러스터의 포인트입니다. 프로토타입과 크리티시즘은 항상 데이터의 실제 인스턴스입니다.

직접 프로토타입을 선택하였음에도, 확장성이 좋지 않아 결과가 좋지 않을 수 있습니다. 데이터에서 프로토타입을 찾는 방법은 여러 방법이 있습니다. 이들 중 하나는 k-means 알고리즘과 관련된 클러스터링 알고리즘인 k-중앙자(k-medoids)입니다. 실제 데이터 포인트를 클러스터 중심으로 반환하는 모든 클러스터링 알고리즘은 프로토타입을 선택할 수 있습니다. 하지만 대부분의 방법은 프로토타입만 찾지만 크리티시즘은 없습니다. 이 장에서는 프로토타입과 크리티시즘을 단일 프레임워크에서 결합하는 접근 방식인 Kim et. al (2016)의 MMD-크리틱(MMD-critic) 에 대해 설명하도록 하겠습니다.
MMD-크리틱은 데이터의 분포와 선택된 프로토타입의 분포를 비교합니다. 이것이 MMD-크리틱의 방법을 이해하기 위한 핵심적인 개념입니다. MMD-크리틱은 두 분포 간의 불일치를 최소화하는 프로토타입을 선택합니다. 특히 다른 "데이터 클러스터"에서 점을 선택하는 경우 밀도가 높은 영역의 데이터 포인트가 좋은 프로토타입입니다. 프로토타입에 의해 잘 설명되지 않는 영역의 데이터 포인트가 크리티시즘으로 선택됩니다.
이제부터 조금 더 이론에 대해 더 깊이 들어가보도고 하겠습니다.
이론
높은 레벨의 MMD-크리틱 절차는 다음과 같이 요약할 수 있습니다.
- 찾고자 하는 프로토타입 및 크리티시즘의 수를 선택합니다.
- 탐욕 알고리즘(Greedy Search)을 통해 프로토타입을 찾습니다. 프로토타입의 분포가 데이터 분포에 근접하도록 프로토타입이 선택됩니다.
- 탐욕 알고리즘으로 크리티시즘을 찾습니다. 프로토타입의 분포와 데이터의 분포가 다른 경우 점을 크리티시즘으로 선택합니다.
MMD-크리틱 데이터셋에 대한 프로토타입과 크리티시즘을 찾으려면 몇 가지 구성요소가 필요합니다. 가장 기본적인 요소로, 데이터 밀도를 추정하기 위한 커널 함수(Kernel Function)가 필요합니다. 커널은 근접성에 따라 두 데이터 포인트의 가중치를 갖는 함수입니다. 밀도 추정치를 바탕으로 선택한 프로토타입의 분포가 데이터 분포에 가까운지 여부를 판단할 수 있도록 두 분포가 얼마나 다른지 알려주는 측정치가 필요합니다. 이는 최대 평균 불일치(Maximum Mean Discrepancy)를 측정함으로써 해결됩니다. 또한 커널 함수를 기반으로 특정 데이터 포인트에서 두 분포가 얼마나 다른지 알려 주는 증거 함수(Witness function)가 필요합니다. 증거 함수를 사용하여 크리티시즘, 즉 프로토타입과 데이터의 분포가 분산되고 증거 함수가 큰 절대값을 차지하는 데이터 포인트를 선택할 수 있습니다. 마지막 요소는 좋은 프로토타입과 크리티시즘에 대한 검색 전략으로, 간단한 탐욕 알고리즘(Greedy Search)으로 해결됩니다.
두 분포 간의 불일치를 측정하는 최대 평균 불일치(MMD)부터 시작해봅니다. 프로토타입을 선택하면 프로토타입의 밀도 분포가 생성됩니다. 프로토타입 분포가 데이터 분포와 다른지 여부를 평가하려 합니다. 커널 밀도 함수를 사용하여 둘 다 추정합니다. 최대 평균 불일치는 두 분포 간의 차이를 측정하며, 이는 두 분포에 따른 기대 간의 함수 공간에 대한 상위 분포입니다. 이제 됐습니다. 개인적으로, 데이터로 어떻게 계산되는지를 볼 때 이러한 개념이 이해가 훨씬 더 잘됩니다. 다음 공식은 MMD 측정값(MMD2)을 계산하는 방법을 나타냅니다.
$$MMD^2=\frac{1}{m^2}\sum_{i,j=1}^m{}k(z_i,z_j)-\frac{2}{mn}\sum_{i,j=1}^{m,n}k(z_i,x_j)+\frac{1}{n^2}\sum_{i,j=1}^n{}k(x_i,x_j)$$
k는 두 점의 유사성을 측정하는 커널 함수이지만, 이는 나중에 더 설명드리겠습니다. m은 프로토타입 z의 수이고 n은 원래 데이터셋의 데이터 포인트 x의 수입니다. 프로토타입 z는 엄선된 데이터 포인트 x입니다. 각 점은 다차원적이므로 여러 기능을 가질 수 있습니다. MMD-크리틱의 목표는 MMD2를 최소화하는 것입니다. MMD2가 0에 가까울수록 프로토타입의 분포가 데이터에 더 잘 맞습니다. MMD2를 0으로 낮추기 위한 핵심은 프로토타입과 다른 모든 데이터 포인트 사이의 평균 근접도를 계산하는 중간의 항입니다(2를 곱함). 이 항이 첫 번째 항(프로토타입 각각의 평균 근접도)과 마지막 항(데이터 포인트 각각의 평균 근접도)에 더해진다면, 프로토타입은 데이터를 완벽하게 설명합니다. 모든 n개의 데이터 포인트를 프로토타입으로 사용할 경우 공식이 어떻게 적용되는지 시험해 보세요.
아래의 그림은 MMD2 측정값을 보여줍니다. 첫 번째 그림에서는 두 가지 특성들이 있는 데이터 포인트를 보여 주며, 데이터 밀도의 추정치는 음영 처리된 배경으로 표시됩니다. 다른 각각의 그림은 그림 제목의 MMD2 측정과 함께 서로 다른 프로토타입 선택 항목을 보여줍니다. 프로토타입은 큰 점이고 분포는 등고선으로 표시됩니다. 이러한 시나리오(왼쪽 아래)에서 데이터를 가장 잘 다루는 프로토타입을 선택하는 경우 불일치 값이 가장 낮습니다.
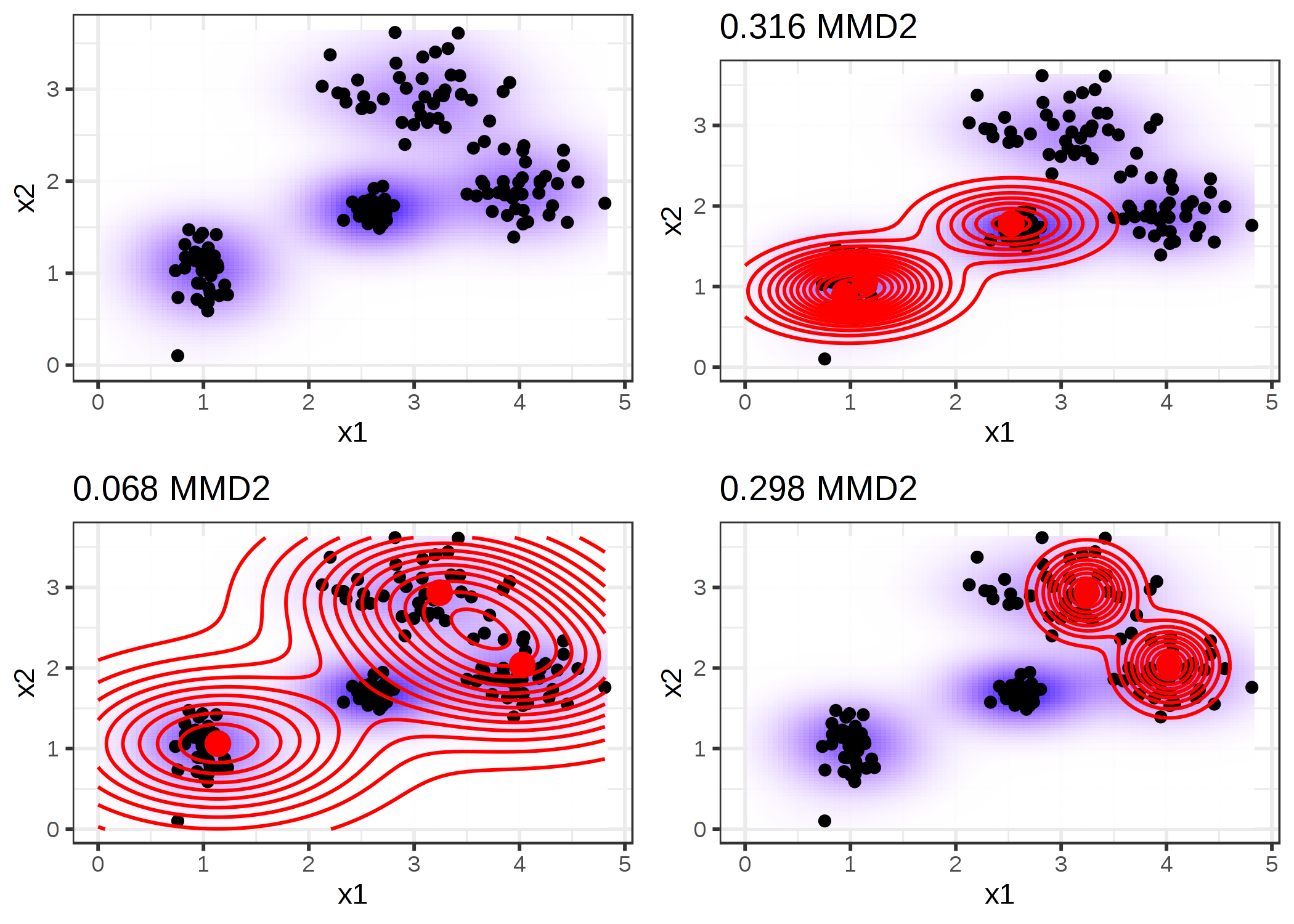
커널의 선택은 방사형 기저 함수 커널입니다.
$$k(x,x^\prime)=exp\left(-\gamma||x-x^\prime||^2\right)$$
여기서 \(||x-x^\prime||^2\)는 두 점 사이의 유클리드 거리이고 γ는 스케일링 매개 변수입니다. 커널값은 두 점 사이의 거리에 따라 감소하며 0과 1 사이의 범위로 두 점이 무한히 멀리 떨어져 있을 때 0, 두 점이 같을 때 1입니다.
MMD2 측정값을 커널 및 탐욕 탐색알고리즘을 프로토타입을 찾기 위한 알고리즘에 결합합니다.
- 비어있는 프로토타입의 리스트에서부터 시작한다.
- While 프로토타입의 수가 선택된 숫자 m 이하일 때:
- 데이터셋 내의 각 포인트에 대해, 해당 포인트를 프로트타입 리스트에 추가했을때 MMD2가 얼마나 줄어드는지 체크한다.
- 프로토타입의 리스트를 리턴한다.
크리티시즘을 찾는 나머지 성분은 특정 포인트에서 두 밀도 추정치가 얼마나 다른지 알려주는 증거 함수입니다. 아래의 식을 사용하여 추정할 수 있습니다.
$$witness(x)=\frac{1}{n}\sum_{i=1}^nk(x,x_i)-\frac{1}{m}\sum_{j=1}^mk(x,z_j)$$
두 데이터셋(특성이 동일)의 경우, 증거 함수는 점 x가 어느 경험적 분포에 더 적합한지를 평가하는 방법을 제공합니다. 크리티시즘을 찾기 위해, 증거 함수의 극값을 양의 방향과 음의방향 모두 찾습니다. 증거 함수의 첫 번째 항은 점 x와 데이터 사이의 평균 근접도이고, 두 번째 항은 점 x와 프로토타입 사이의 평균 근접도입니다. 점 x에 대한 증거 함수가 0에 가까우면 데이터의 밀도 함수와 프로토타입의 분포가 점 x에 있는 데이터의 분포와 유사하다는 것을 의미합니다. 점 x에 있는 음의 증거 함수는 프로토타입 분포가 데이터 분포를 과대평가한다는 것을 의미합니다(예를 들어, 프로토타입을 선택했지만 근처에 데이터 포인트가 거의 없는 경우), 즉 점 x의 양의 증거 함수는 프로토타입 분포가 데이터 분포를 과소평가한다는 것을 의미합니다(예: x 주위에 데이터 포인트가 많지만 근처에 프로토타입을 선택하지 않은 경우).
좀 더 직관적으로, 가장 낮은 MMD2로 미리 플롯의 프로토타입을 재사용하고 수동으로 선택한 몇 가지 포인트에 대한 증거 함수를 표시합니다. 프로토타입과 크리티시즘은 기계학습 모델과 독립적으로 데이터를 기술하는 데 사용될 수 있지만, 해석할 수 있는 모델을 만들거나 블랙박스 모델을 해석할 수 있는 모델로 만드는 데도 사용할 수 있습니다.

증거함수를 사용하면 프로토타입으로 잘 표현되지 않는 데이터 인스턴스를 명시적으로 검색할 수 있습니다. 크리티시즘은 증거함수에서 절대적 가치가 높은 포인트입니다. 프로토타입과 마찬가지로 크리티시즘도 탐욕 검색을 통해 발견됩니다. 그러나 전체 MMD2를 줄이는 대신 증거함수와 정규화 항을 포함하는 비용 함수를 최대화하는 점을 찾고 있습니다. 최적화 함수의 추가 항은 포인트의 다양성을 적용하므로 점이 서로 다른 클러스터로부터 나오도록 해야 합니다.
이 두 번째 단계는 프로토타입을 찾는 방법과 무관합니다. 저자 또한 몇몇 프로토타입을 직접 골라서 여기에 설명된 절차를 이용해 프로토타입을 배울 수도 있었습니다. 또는 프로토타입은 k-medoid와 같은 클러스터링 절차에서 나올 수도 있습니다.
이것이 MMD-크리틱 이론의 중요한 부분입니다. 한 가지 질문이 남아 있습니다. MMD-크리틱은 해석 가능한 기계 학습에서 어떻게 사용될 수 있을까요?
MMD-크리틱은 다음 세 가지 방법으로 해석력을 추가할 수 있습니다.
- 데이터 분포를 더 잘 이해할 수 있도록 돕고
- 해석 가능한 모형을 만들고
- 블랙박스 모형을 해석할 수 있게 합니다.
MMD-크리틱을 데이터에 적용하여 프로토타입과 크리티시즘을 찾는 경우, 특히 가장자리 케이스가 포함된 복잡한 데이터 분포가 있는 경우 데이터에 대한 이해도를 높일 수 있습니다. 하지만 MMD-크리틱으로 여러분은 더 많은 것을 얻을 수 있습니다!
예를 들어, 해석 가능한 예측 모델, 이른바 "가장 가까운 프로토타입 모델"을 생성할 수 있습니다. 예측 함수는 다음과 같이 정의됩니다.
$$\hat{f}(x)=argmax_{i\in{}S}k(x,x_i)$$
즉, 프로토타입을 새로운 데이터 포인트에 가장 가까운 S 프로토타입을 선택하여 커널 함수의 가장 높은 값을 산출합니다. 프로토타입 자체는 예측에 대한 설명으로 반환됩니다. 이 절차에는 세 가지 조정 매개 변수가 있습니다. 커널 유형, 커널 확장 매개 변수 및 프로토타입 수입니다. 교차 검증 루프 내에서 모든 매개 변수를 최적화할 수 있습니다. 크리티시즘은 이 접근법에서 사용되지 않습니다.
세 번째 옵션으로, MMD-크리틱을 사용하여 모델 예측과 함께 프로토타입과 크리티시즘 내용을 조사하여 모든 기계학습 모델을 전체적으로 설명할 수 있게 할 수 있습니다. 절차는 다음과 같습니다.
- MMD-크리틱과 함께 프로토타입과 크리티시즘을 찾는다.
- 평소와 같이 기계학습 모델을 학습시킨다.
- 기계학습 모델로 프로토타입과 크리티시즘에 대한 결과값을 예측한다.
- 알고리즘에 문제가 생긴 경우를 감안하여 예측값을 문석한다. 지금 여러분은 그 데이터를 잘 대표하는 많은 예제를 갖고 있으며, 이는 이 기계학습 모델의 약점을 발견하는 것을 도와준다.
지금까지의 내용들이 여러분들께 도움이 되었을까요? 구글의 이미지 분류기가 흑인을 고릴라로 식별한 것을 기억하시나요? 이미지 인식 모델을 배포하기 전에 여기에 설명된 절차를 사용해야 했을 수도 있습니다. 모델 성능이 99% 정확하다면 해당 문제가 여전히 1%에 해당될 수 있기 때문에 단순히 모델 성능을 점검하는 것만으로는 충분하지 않습니다. 그리고 Label도 틀릴 수 있습니다! 모든 학습 데이터를 검토하고 예측에 문제가 있는지 순결성 검사를 수행하면 문제가 드러났을 수 있지만 실현 불가능하게 됩니다. 그러나 수천 개의 프로토타입과 크리티시즘의 선택은 실현 가능하며 데이터에 문제가 있을 수 있습니다. 어두운 피부를 가진 사람들의 이미지가 부족하다는 것을 보여주었을 수 있는데, 이것은 데이터셋의 다양성에 문제를 나타냅니다. 아니면 그것은 원형으로 어두운 피부를 가진 사람의 하나 이상의 이미지를 보여주거나 악명 높은 "고릴라" 분류를 가진 크리티시즘의 이미지를 보여주었을 수도 있습니다. MMD-크리틱이 이런 종류의 실수를 확실히 막아줄 것이라고 약속하지는 않지만, 이는 좋은 순결성 검사 방법이라 할 수 있습니다..
예제
MMD-critic의 다음 예제에서는 손으로 쓴 숫자의 데이터를 사용합니다.
실제 프로토타입을 보면 이미지의 숫자와 번호가 다르다는 것을 눈치 챌 수 있습니다. 때문에 프로토 타입은 정해진 수의 전체 데이터셋을 넘나들며 검색하는 것이 아니라 클래스당 정해진 번호로 검색되된 것입니다. 이는 예상대로, 프로토 타입은 숫자를 쓰는 다른 방법을 보여 줍니다.

장점
사용자 연구(User study)에서 MMD-크리틱의 저자들은 참가자들에게 이미지를 주었고, 그들은 각각 두 개의 클래스 중 하나를 나타내는 두 개의 이미지셋 중 하나에 시각적으로 일치시켜야 했습니다(예: 두 종의 개 품종). 참가자들은 셋이 클래스의 임의의 이미지 대신 프로토타입과 크리티시즘으로 나타날 때 최상의 성능을 보였습니다.
프로토타입과 크리티시즘의 수를 자유롭게 선택할 수 있습니다.
MMD-크래틱은 데이터의 밀도 추정과 함께 동작합니다. 이는 어느 타입의 데이터와 어느 타입의 기계학습에서 동작합니다.
이 알고리즘은 적용하기가 쉽습니다.
MMD-크리틱은 해석력을 높이는 데 사용되는 방식으로 매우 유연합니다. 복잡한 데이터 분포를 이해하는 데 사용할 수 있습니다. 해석 가능한 기계 학습 모델을 구축하는 데 사용할 수 있습니다. 또는 블랙박스 기계 학습 모델의 의사결정에 대해 밝힐 수 있습니다.
크리티시즘을 찾는것 프로토타입의 선택 과정과는 무관합니다. 그러나 MMD-크리틱에 따라 프로토타입을 선택하는 것이 타당합니다. 프로토타입과 크리티시즘은 동일한 방식으로 프로토타입과 데이터 밀도를 비교하기 때문입니다.
단점
프로토타입과 크리티시즘은 수학적으로 다르게 정의되지만, 그 차이는 컷오프 값(프로토타입의 수)을 기반으로 합니다. 데이터 분포를 포함하기에 너무 적은 수의 프로토타입을 선택했다고 가정합니다. 그 크리티시즘들은 그렇게 잘 설명되지 않는 부분에서 끝날 것입니다. 하지만 프로토타입을 더 추가한다면 동일한 영역에 속하게 될 것입니다. 모든 해석은 크리티시즘이 기존 프로토타입과 (임의) 컷오프 값에 크게 좌우된다는 점을 고려해야 합니다.
프로토타입의 수와 크리티시즘의 수를 선택해야 합니다. 이것이 좋은 것이 될 수 있는 만큼 단점도 있습니다. 실제로 얼마나 많은 프로토타입과 크리티시즘이 필요할까요? 많을수록 좋을까요? 적을수록 좋을까요? 한 가지 해결책은 특정 응용 분야에 따라 달라지는 이미지를 보는 작업에 사람이 얼마나 많은 시간을 할애할 수 있는지를 측정하여 프로토타입과 크리티시즘의 수를 선택하는 것입니다. MMD-크리틱을 사용하여 분류기를 작성할 때만 직접 최적화할 수 있습니다. 한 가지 해결책은 x축의 프로토타입 수와 y축의 MMD2 측정값을 보여주는 그래프일 수 있습니다. 아마도 MMD2 곡선이 평평해지는 프로토타입데이터를, 큰 점은 크리티시짐을, 그리고 그보다 큰 정사각형은 프로토타입입니다. 프로토타입은 데이터 분포의 중심을 커버하기 위해 (수동적으로) 선택되며, 크리티시즘은 프로토타입이 없는 클러스터의 포인트입니다. 프로토타입과 크리티시즘은 항상 데이터의 실제 인스턴스입니다.
다른 매개 변수는 커널과 커널 확장 매개 변수의 선택입니다. 프로토타입 수 및 크리티시즘과 동일한 문제가 있습니다. 커널 및 해당 확장 매개 변수를 선택하려면 어떻게 해야 할까요? 다시, MMD-크리틱을 가장 가까운 프로토타입 분류기로 사용할 때, 우리는 커널 매개 변수를 조정할 수 있습니다. 그러나 MMD-크리틱의 비지도(Unsupervised) 사용 사례에 대해서는 명확하지 않습니다. (모든 비지도 방법에는 이런 문제가 있기 때문에, 여기서 약간 냉혹할 수 있습니다.)
일부 특성이 관심 결과 예측과 관련이 없을 수 있다는 사실을 무시하고 모든 특성을 입력으로 사용합니다. 한 가지 해결책은 원본 픽셀 대신 이미지 임베딩과 같은 관련 특성만 사용하는 것입니다. 이 작업은 관련 정보만 포함된 표현에 원본 인스턴스를 투영할 수 있는 경우에만 동작합니다.
사용할 수 있는 코드가 몇 가지 있지만, 패키징 및 문서화된 소프트웨어만큼 잘 구현되어 있지 않습니다.
코드 및 대안
MMD-크리틱의 구현에 대한 내용은 아래 사이트를 참조해 주시길 바랍니다.
https://github.com/BeenKim/MMD-critic
BeenKim/MMD-critic
Contribute to BeenKim/MMD-critic development by creating an account on GitHub.
github.com
프로토타입을 찾는 가장 간단한 대안은 Kaufman et. al(1987)의 k-medoids입니다.
참고자료: christophm.github.io/interpretable-ml-book/proto.html
6.3 Prototypes and Criticisms | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 6. 예제 기반 설명' 카테고리의 다른 글
| [해석할 수 있는 기계학습(6-4)]영향력 있는 인스턴스(Influential Instances) (0) | 2021.04.05 |
|---|---|
| [해석할 수 있는 기계학습(6-2)]적대적 예제(Adversarial Examples) (1) | 2021.02.04 |
| [해석할 수 있는 기계학습(6-1)]반사실적 설명(Counterfactual Explanations) (0) | 2021.01.30 |
| [해석할 수 있는 기계학습(6-0)] 예제 기반 설명(Example-Based Explanations) (0) | 2020.12.01 |




