늦깎이 공대생의 인공지능 연구실
ICML Tutorial on Model-Based Methods in Reinforcement Learning(모델 기반 강화학습) - 2.모델 기반 제어 본문
ICML Tutorial on Model-Based Methods in Reinforcement Learning(모델 기반 강화학습) - 2.모델 기반 제어
Justin T. 2022. 9. 4. 23:58
지금까지 다음과 같은 대표적인 알고리즘을 포함하여 현존하는 다양한 알고리즘과 카테고리의 배경을 사용할 것입니다.

앞서 살펴본 것처럼, 우리는 세 가지 방법으로 모델을 사용할 수 있습니다. 이어서 각 사례에 대한 몇 가지 예를 살펴보겠습니다.

환경 시뮬레이션(Simulating the environment)
한 가지 방법은 실제 데이터를 모델에서 생성된 경험(Experience)과 혼합한 다음 Q-러닝, 정책 기울기 등과 같은 기존의 모델이 없는 알고리즘을 적용하는 것입니다. 이 경우 모델은 더 크고 강화된 학습 데이셋을 제공합니다.
Dyna-Q는 학습된 모델과 함께 Q-러닝을 사용하는 예입니다. Dyna는 실제 전이(Transition)에 대한 기존 Q-러닝 업데이트를 수행하고 모델을 사용하여 실제 상태에서 가상의 전이를 생성하고 이러한 상태에 대해 동일한 Q-러닝 업데이트를 수행합니다. 그래서 기본적으로 경험을 늘리는 방법외에는 마땅한 방법이 없습니다.

이는 정책 학습(Policy Learning)에도 적용될 수 있습니다. 실제 데이터에서 훨씬 더 멀리 떨어진 경험을 생성하고 이러한 가상 경험에 대한 정책 매개 변수 업데이트를 전적으로 수행하기 위해 모델에 따라 한 단계만 수행하는 것이 아니라 여러 단계를 수행할 필요가 있습니다.

학습 알고리즘 지원
이를 위한 한 가지 중요한 방법은 모델을 통해 종단 간 학습(End-to-end training)을 허용하는 것입니다. 최근 컴퓨터 비전, NLP 등에서 지도 학습 방법을 개선하고 단순화하는데 있어 종단 간 학습이 매우 성공적이었습니다.
문제는 "우리는 동일한 유형의 종단 간 접근 방식을 RL에도 적용할 수 있는가?"입니다.
한 가지 예로 정책 기울기 알고리즘이 있습니다. 예를 들어 일부 매개변수 정책의 할인된 미래 보상(Discounted future reward)의 합을 최대화하려고 합니다. 정책 파라미터 θ에 대한 목적 함수를 다음과 같이 나타낼 수 있습니다.
$$J(\theta)=\sum_{t=0}^{\infty }\gamma^{t}R(s_{t},a_{t}),\quad a_{t}=\pi_{\theta}(s_{t}),\quad s_{t+1}=T(s_{t},a_{t})$$
이제 정책 매개 변수 θ와 관련하여 정책 기울기에 경사 상승(최대화를 위해)을 다음과 같이 적용해야 합니다.
$$\theta\to \bigtriangledown _{\theta}J$$
그렇다면 \(\bigtriangledown _{\theta}J\)을 어떻게 계산할 수 있을까요?
이 기울기를 추정하기 위해 REINFORCE와 같은 샘플링 기반 방법이 제안되었습니다. 하지만 문제는 이 방법이 매우 큰 편차를 가질 수 있다는 것과, 결정을 내리는데 있어 정책이 어느 정도 무작위성을 요구한다는 것입니다. 이것은 적합하지 않을 수 있습니다.

다음 솔루션은 정확하고 매끄러운 모델입니다. 정확하고 매끄러운 모델은 가상의 경험 외에도 미분을 제공합니다.
$$s_{t+1}=f_{s}(s_{t},a_{t})\quad r_{t}=f_{r}(s_{t},a_{t})\\
\triangledown _{s_{t}}(s_{t+1}),\quad \triangledown _{a_{t}}(s_{t-1}),\quad \triangledown _{s_{t}}(r_{t}),\quad \triangledown _{a_{t}}(r_{t}),\quad \cdots $$
그리고 이 식들은 다음과 같은 질문에 대답할 수 있습니다: 행동의 작은 변화가 다음 상태를 변화시키거나 다른 수치에 대해 보상할 수 있을까요?

이는 왜 유용할까요? 이는 역전파(Back-propagation)와 같은 이러한 유형의 종단간 미분 알고리즘을 수행할 수 있기 때문에 유용합니다.
모델을 사용하여 우리만의 목표 함수를 다시 작성해봅니다.
$$J(\theta )\approx \sum_{t=0}^{H}\gamma ^{t}r_t,\quad a_t=\pi _\theta (s_t),\quad s_{t+1}=f_s(s_t,a_t),\quad r_t=f_r(s_t,a_t)$$
그럼 어떻게 이 도함수를 사용하여 \(\triangledown _\theta J\)를 계산할 수 있을까요?

강조된 도함수는 PyTorch 또는 TensorFlow와 같은 일부 라이브러리를 사용하여 쉽게 계산할 수 있습니다.
이러한 방법으로 \(\triangledown _\theta J\)를 계산했을 때
장점:
- 우리가 얻는 정책 기울기는 사실 결정된 값이며, 이에 대한 편차는 없습니다.
- 잠재적으로 훨씬 더 장기적인 신용 할당 문제(Credit Assignment Problem) 지원할 수 있습니다.
단점:
- 지역 최소값(Local minima)에 빠질 수 있습니다.
- 컨디셔닝이 그리 좋지 않습니다.(기울기의 사라짐/폭발)
다음은 실수 또는 모델 생성 궤적을 따라 모델 기반 역전파(미분)를 사용하여 종단간 학습을 수행하는 두 가지 예제입니다.
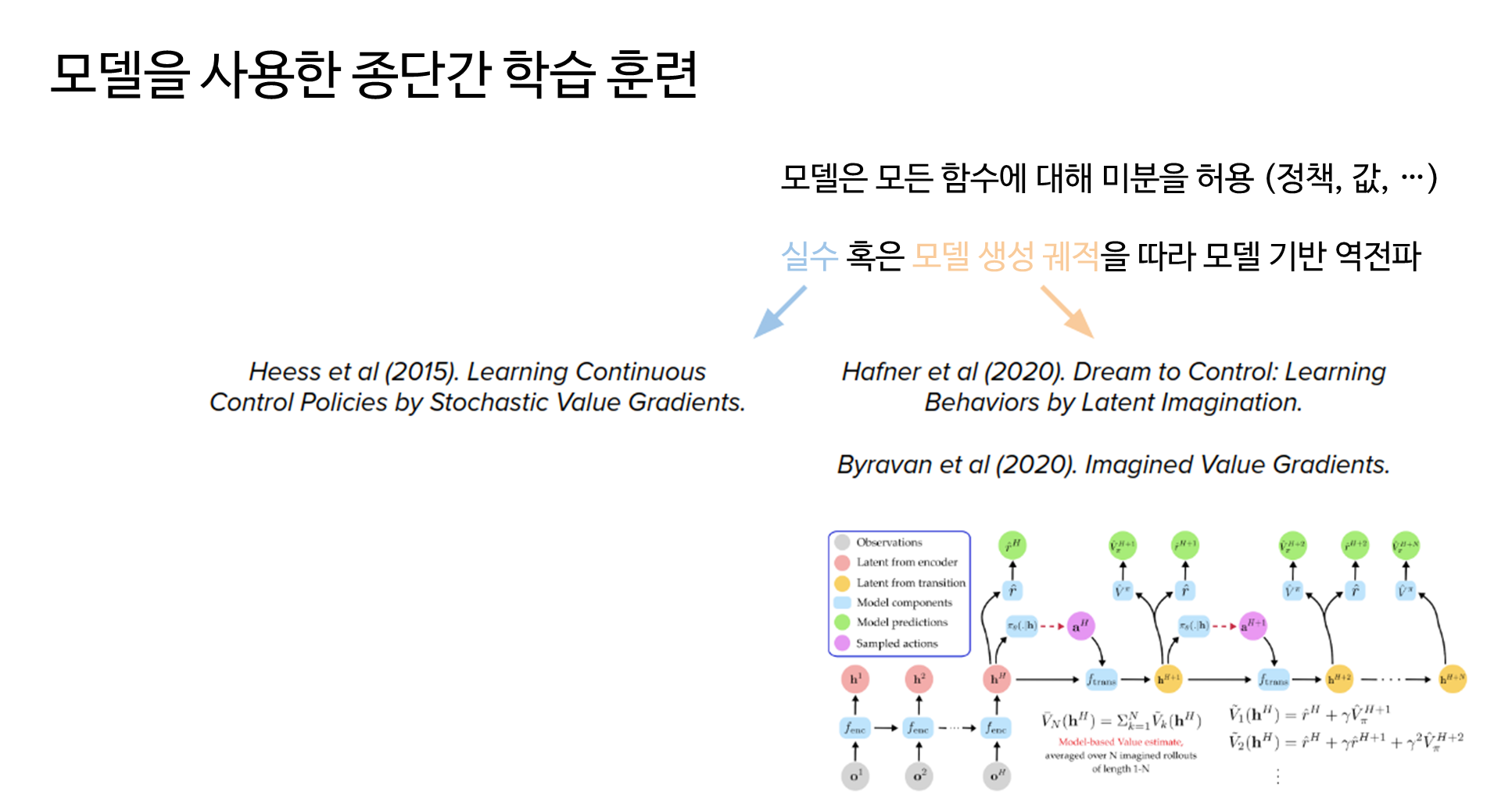
- 실제 궤적이 더 안전하지만 현재 정책 매개 변수에서 추출해야 합니다(샘플 효율성이 떨어짐).
- 모델 생성 궤적은 실제와 상호 작용하지 않고 더 큰 정책 변경을 허용하지만 모델 부정확성으로 인해 더 큰 어려움을 겪을 수 있습니다.
정책 강화
지금까지 RL에서 모델을 사용하는 첫 두 가지 방법에 대해 이야기 해보았습니다. 이 두 가지 방법은 배경 계획(Background Planning)의 카테고리에 속합니다.
Sutton and Barto(2018)의 논문에 따르면 강화학습에 기반한 또다른 카테고리가 있습니다.
강화학습은 카테고리화의 도입으로서 Decision-Time Planning(의사결정 시간 계획)이라 하며, 이는 모델 기반 설정에서 가능한 독특한 옵션입니다.
배경 계획(Background Planning)과 의사결정 시간 계획(Decision-Time Planning)의 차이는 무엇일까요?
배경 계획(Background Planning)의 관점에서 우리는 "모든 행동 가능한 상횡에서 목적에 도달하는데 성공하는 행동을 어떻게 행할 수 있는지를 어떻게 배울 수 있을까"와 같은 질문에 답을 생각할 수 있습니다.

- 최적화 변수는 정책, 가치 함수 또는 기타 등등의 매개 변수이며 가능한 모든 상황에 대한 기대치를 사용하여 학습합니다.
- 개념적으로, 우리는 배경 계획(Background planning)을 우리가 재사용할 수 있는 일련의 습성들을 배우는 것으로 생각할 수 있습니다.
- 우리는 배경 계획이 빠른 사고방식을 배우는 것으로 생각할 수 있습니다.
의사결정 시간 계획 관점에서, 우리는 "현재 나의 상황을 성공시키거나 목표에 도달하기 위한 최선의 행동 순서는 무엇인가?"라는 질문에 대한 답을 원합니다.
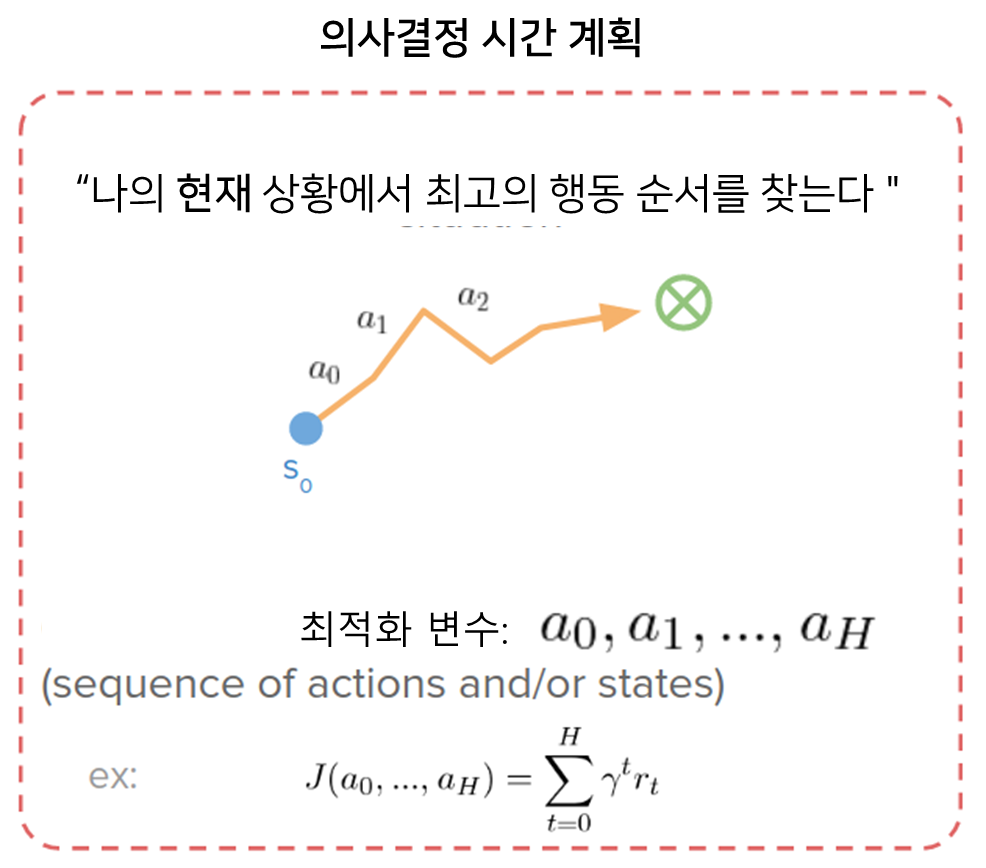
- 최적화 파라미터는 일련의 동작 또는 상태에 불과합니다.
- 개념적으로, 우리는 의사결정 시간 계획을 단지 우리가 처한 특정한 상황에 대해 의식적으로 즉흥적인 것을 발견하는 것으로 생각할 수 있습니다.
- 우리는 의사결정 시간 계획을 느린 사고의 유형을 배우는 것으로 생각할 수 있습니다.
왜 두 종류의 계획 방식을 써야 할까요?

- 가장 최근의 상황에 따라 동작 수행: 의사결정 시간 계획은 단지 일련의 행동을 찾는 데 있어서 현재 상태에 대해서만 관심을 둡니다. 여러분은 가장 최근의 World 상태에 따라 행동할 수 있습니다. 반대로 배경 계획에서는 습관이 오래되어 World의 변화에 따라 업데이트되는 데 시간이 걸릴 수 있습니다.
- 아무 학습 없이 동작 수행: 의사결정 시간 계획은 우리가 전혀 배운것 없이 행동할 수 있게 해줍니다. 우리가 결정을 내리기 전까지는 정책이나 가치 신경망을 필요로 하지 않습니다. 여러분이 모델을 가지고 있는 한 그것은 단지 최적화 문제일 뿐입니다.
- 익숙하지 않은 상황에서 능숙함: 만약 여러분이 학습하고 있던 곳에서 멀리 떨어진 상황에 처해 있게 된다면, 여러분의 습관이나 정책 신경망은 그곳에서 능력(성공적이거나 효율적으로 무언가를 할 수 있는 능력)을 갖지 못할 수도 있습니다. 따라서 행동할 정보가 없거나, 매우 불확실하거나, 최악의 경우조차, 확신을 가지고 말이 안 되는 결정을 내릴 수 있습니다. 이것은 분포와 일반화 문제에서 벗어납니다. 이러한 경우, 의사결정 시간 계획이 더 유익할 것입니다.
- 관측 공간과는 독립적: 의사결정 시간 계획의 또 다른 장점은 사용자가 결정한 관측 공간과도 무관하다는 것입니다. 배경 방법에서는 정책 함수에 상태, 결합 각도 또는 픽셀이나 그래프의 인코딩이나 설명을 고려해야 합니다. 이러한 결정은 전체 학습 성과에 큰 역할을 할 수 있습니다. 어떤 것이 작동하지 않을 때는 충분한 정보를 포함하고 있지 않은 알고리즘이나 상태 공간 때문에 그런 것인지 잘 알 수는 없습니다. 이와는 대조적으로 의사결정 시간 계획은 이러한 혼동을 방지하므로 실제로 새로운 방법을 프로토타입화할 때 매우 유용합니다.

- 부분적 관찰 가능: 의사결정 시간 계획에는 몇 가지 문제가 있습니다. 이 계획은 여러분이 계획을 세울 때 여러분이 World의 모든 상태를 안다고 가정합니다. 그래서 의사결정 시간 계획에게 있어 정보를 숨기는 것은 어렵습니다. 가능은 하지만 비용이 더 많이 듭니다.
- 실제 사용시 빠른 계산 속도: 의사결정 시간 계획은 더 많은 계산시간이 필요합니다. 단순히 습관을 평가하는 것이 아니라 더 많은 생각을이 필요로 합니다.
- 예측가능성및 일관성: 의사결정 시간 계획은 반드시 예측 가능하거나 일관적이지 않은 몇 가지 행동을 합니다. 여러분은 의식적으로 각각의 스탭에 대해 생각하고 있기 때문에, 여러분들은 정확히 같은 계획을 가지고 있지 않을 수도 있습니다. 그래서 여러분은 여전히 성공하는 매우 혼란스러운 행동을 할 수도 있습니다. 반대로, 배경 계획은 일련의 습관을 배우기 때문에 매우 규칙적인 행동을 할 수 있습니다.
- 이산적이고 연속적인 행동에도 동일함: 배경계획은 이산적이고 연속적인 행동들을 매우 통일적으로 다루는데, 이것은 개념적으로 더 간단합니다. 의사결정 시간 계획에는 이산적이고 연속적인 행동을 위한 다른 알고리즘이 있습니다. 우리는 그것들에 대해 아래에서 더 자세히 알아보겠습니다.
우리는 또한 배경 계획과 의사결정 시간 계획을 혼합하거나 일치시킬 수 있습니다.
이산형 계획과 연속형 계획의 차이점은?
문제를 해결하고자 할 때 이산형 계획과 연속형 계획 중 어떤 방법으로 해결할지는 여러분들이 해결하고자 하는 문제에 따라 다릅니다. 그렇기에 여러분들은 선택의 고민을 할 이유가 없습니다. 예를 들어 로봇을 제어할 때 동작은 모터의 토크가 될 수 있고(연속), 생체역학 설정에서는 근육 자극(연속), 또는 의료 문제에서는 적용되어야 하는 치료(이산)일 수 있습니다.
배경 계획 방법에서 이산 행동과 연속 행동 간의 차이는 중요하지 않습니다.
- 여러분들은 단지 이산형 분포 또는 연속형 분포에서 표본을 추출하는 확률적 정책을 학습합니다.
$$a\sim \pi (.|s) \quad \leftarrow Gaussian,categorical,...$$
- 역전파는 일부 재매개변수화(Reparametrization) 기술을 통해 여전히 가능합니다. Jang et al(2016) 논문 참조. 예를 들어 Gumbel-Softmax를 사용한 카테고리형 재매개변수화를 참조.
이러한 두 가지 경우(연속적이고 이산적인 배경 계획 방법)에서 기대치를 초과하여 최적화하기 때문에 최종 목표 및 최적화 문제는 여전히 정책 매개변수를 부드럽게 합니다.
- 역전파는 일부 재매개변수화 기술을 통해 여전히 가능합니다. Jang et al(2016)을 참조. 예를 들어 Gumbel-Softmax를 사용한 카테고리형 매개 변수화를 참조.
이러한 경우(배경 계획 방법에서 연속적이고 이산적인 경우) 기대 이상의 최적화를 수행하므로 최종 목표 및 최적화 문제는 여전히 정책 매개 변수를 원활하게 작성할 수 있습니다.
$$J(\theta)=E_{\pi}[\sum_tr^t],\quad a_t\sim\pi(.|s_t,\theta)$$
그러나 의사결정 시간 계획(Decision-Time Planning)의 경우, 이러한 구별은 이산 검색 또는 연속 궤적 최적화와 같은 이산 행동(Discrete Actions) 그리고 연속 행동(Continuous Action)에 대한 전문화된 방법을 이끌어냅니다.
몇 가지 예를 들어 비교해 보겠습니다.
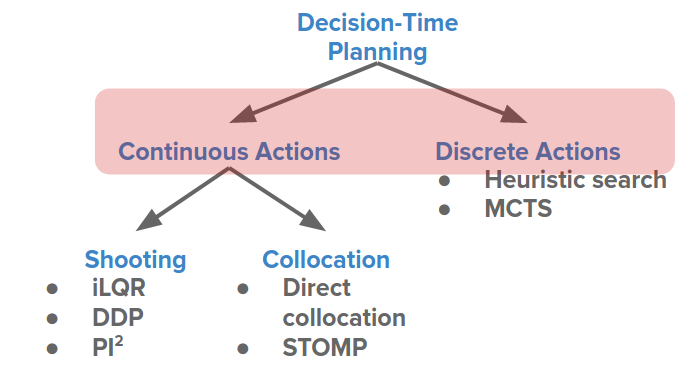
MCTS(몬테 카를로 트리 검색)
이 알고리즘은 이산 행동 그룹에 속하며 알파고와 알파 제로에서 사용됩니다. 고려해야 할 모든 상태와 작업에 대해 장기 보상인 Q-값을 추적합니다. 또한 이전에 상태(state) 및 행동(action)을 수행한 횟수입니다.
1. \( Q_0(s,a) = 0, N_0 = (s,a), k = 0\) 으로 초기화 합니다.
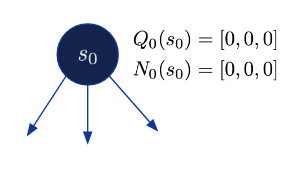
2. 확장: 현재 상태에서 시작하여 노드를 확장하고 검색 정책에 따라 작업을 선택합니다.
$$\pi_{k}(s)=Q_{k}(s,a)$$

3.평가: 새 노드에 도달하면 Monte-Carlo 롤아웃을 사용하여 장기 가치(Long-term Value)를 추정합니다.

4.백업: Q값을 상위 노드에 전파합니다.
$$Q_{k+1}(s,a)=\frac{Q_k(s,a)+R}{N_k(s,a)+1}$$
$$N_{k+1}=N_k(s,a)+1$$
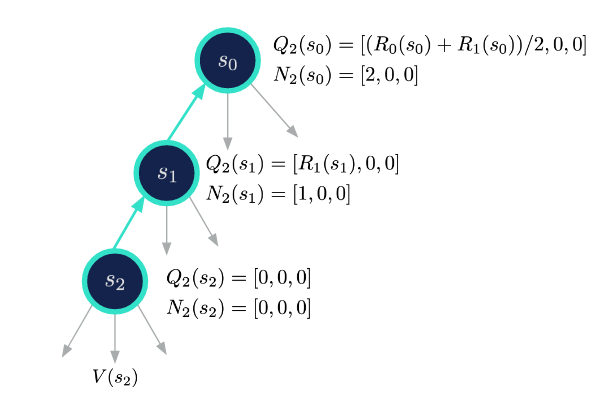
5. 2-4단계를 반복합니다.

궤적 최적화
여러 가지 가능성이 있는 트리를 추적하는 대신 하나의 가능한 행동 시퀀스를 추적합니다.
1. 추측으로 \(a_0,...,a_H\) 를 초기화 합니다.

2. 확장: 상태 순열 \(s_1,...,s_H\)를 얻기 위해 행동 순열 \(a=a_0,...,a_H\)를 실행합니다.

3. 평가: 궤적 보상 \(J(a)=\sum_{t=0}^Hr_t\)를 얻습니다.
4. 역전파: 모든 값이 미분 할 수 있으므로, 보상 모델 미분과 전이 모델 미분을 이용하여 보상의 기울기를 계산하면 됩니다.
$$\triangledown_aJ=\sum_{t=0}^H\triangledown_ar_t$$
$$\triangledown_ar_t=\triangledown_sf_r(s_t,a_t)\triangledown_as_t+\triangledown_af_r(s_t,a_t)$$
$$\triangledown_as_t=\triangledown_af_s(s_{t-1},a_{t-1})+\triangledown_sf_s(s_{t-1},a_{t-1})\triangledown_as_{t-1}$$
$$\triangledown_as_{t-1}=...$$
5. 모든 행동 a를 \(a\leftarrow a+\triangledown_aJ\)으로 기울기를 향상시켜 업데이트 하고 2~5를 반복합니다.

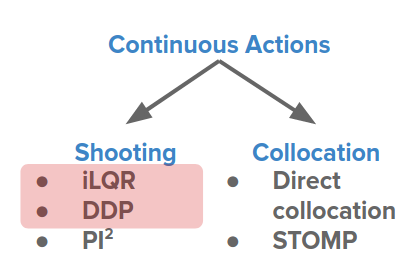
이산 행동과 연속 행동의 차이는 다음과 같이 요약할 수 있습니다.

위에서 본 연속 방식은 사격법(Shooting method)으로 분류할 수 있습니다.
연속 계획 방법의 다양성과 동기부여
다음과 같은 문제를 완화하기 위해 다양한 방법이 시도되고 있습니다.
- 민감성과 나쁜 조건(Sensitivity and poor conditioning)
- 지역 최적값만에 도달(Only reaches local optimum)
- 느린 수렴(Slow convergence)
서로 다른 종류의 방법으로 이어지는 행동 과정을 그림으로 다음과 같이 나타낼 수 있습니다.

민감성과 나쁜 조건(Sensitivity and poor conditioning)
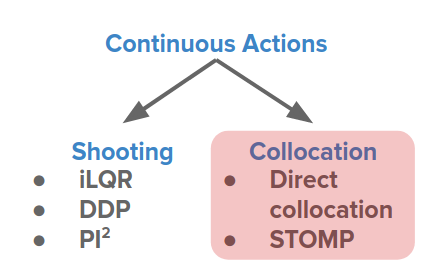
우리가 보았던 사격법(Shooting method)은 초기 행동의 작은 변화가 다운스트림의 매우 큰 변화로 이어진다는 특별한 문제를 가지고 있습니다.
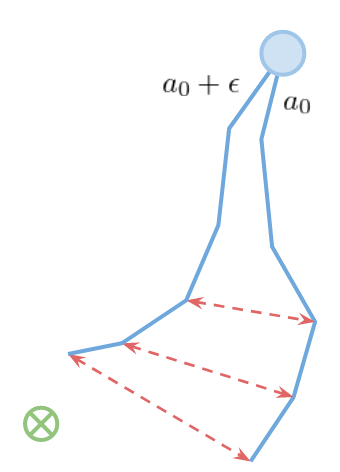
목표 함수를 확장함으로써, 이는 더 명료하게 이해할 수 있습니다.
$$\max_{a_0,...,a_H}\sum_{t=0}^Hr(s_t,a_t),\quad s_{t+1}=f(s_t,a_t)$$
$$\sum_{t=0}^Hr(s_t,a_t)=r(s_0,a_0)+r(f(s_0,a_0),a_1)+...+r(f(f(...),...),a_H)$$
이는 각 상태가 암묵적으로 그 이전의 모든 행동에 의존한다는 것을 의미합니다. 이는 장기 기여도 부여(Long-term credit assignment)를 해치는 RNN의 폭발적/소멸적 그레이디언트 문제와 유사합니다. 그러나 RNN 학습과는 달리 환경에 의해 우리에게 요구되기 때문에 전이 함수를 변경할 수 없습니다.

이 문제를 해결하기 위해 행동만 아닌 상태 혹은 행동에 대해 직접 최적화하는 Collocation(연계)이 도입되었습니다. 그래서 우리는 우리가 최적화하고 있는 다른 매개변수들을 가지고 있습니다.
\(\max_{s_0,a_0,...,s_H,a_H}\sum_{t=0}^Hr(s_t,a_t),\quad ||s_{t+1}-f(s_t,a_t)||=0\leftarrow\) explicit optimization constraint
이는 사격법과 같이 시공만으로 만족하기보다는 명시적으로 제한된 최적화 문제입니다.
따라서 이전 그림의 사격법에 대한 조밀한 활동 그래프와 달리 변수 간에 쌍별 종속성만 있을 수 있습니다.
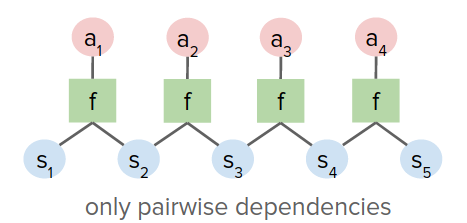
이 방법은 다음과 같은 속성을 갖고 있습니다.
- 좋은 조건(Good Positioning): \(s_0, a_0\)을 변경하는 것은 \(s_H, a_H\)을 변경하는 것과 유사합니다.
- 더 크지만 검색 공간을 최적화하기 쉽습니다. 일부 로봇 응용 프로그램과 같이 접촉이 많은 문제에 유용합니다.
지역 최적값만에 도달(Only reaches local optimum)
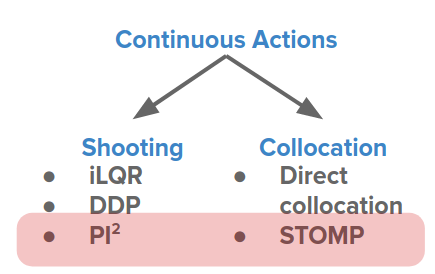
일부 접근 방식은 샘플링 기반 방법인 크로스 앤트로피 방법(CEM) 및 \(PI^2\)와 같은 지역최적화를 피하려고 합니다.
예를 들어, CEM에서는 최적 궤적을 유지하는 대신 최적 궤적의 평균과 공분산을 유지합니다.

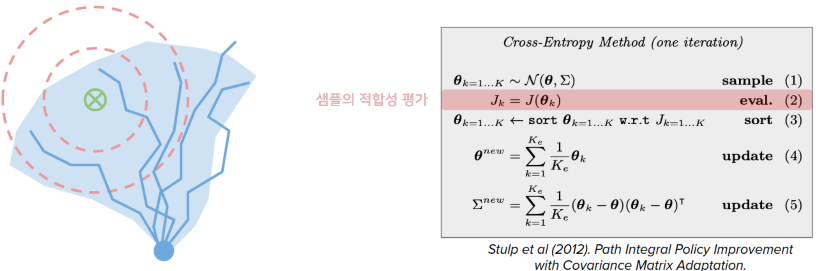
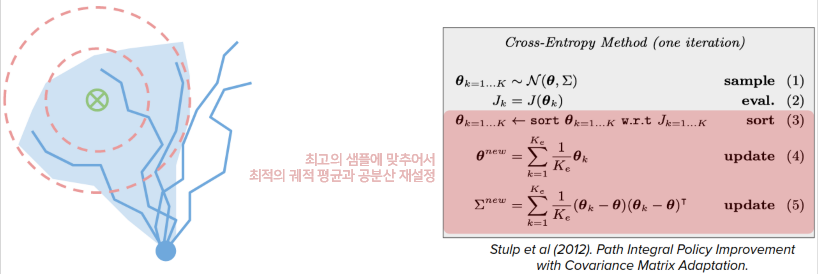
매우 간단함에도 불구하고, 이것은 놀라울 정도로 잘 작동하며 성능에 대한 매우 좋은 보증을 제공합니다. 왜 그런지 확인해볼까요?
- 정책 매개 변수 공간보다 훨씬 작은 의사결정 시간 계획의 탐색 공간: ex. 30x32 vs 32x644x32
- 정책 매개 변수보다 더 많은 실행 가능한 계획
느린 수렴(Slow convergence)
경사하강법은 수렴하기에 너무 느리고, 정책을 훈련시키기 위해 수천만 번을 기다려야 합니다. 하지만 이는 우리가 학습을 끝내고 싶어하는 일회성 계획으로는 상당한 시간이 걸립니다.
궤도 최적화를 위한 뉴턴 방법(Newton's method), 비선형 최적화 같은 것을 할 수 있습니다. 선형 함수로 전이를 근사화하고 사분법으로 보상을 계산할 수 있습니다.
$$\max_{s_0,a_0,...,s_H,a_H}\sum_{t=0}^Hr_t,\quad s_{t+1}=f_s(s-t,a_t),\quad r_t=f_r(s_t,a_t)$$
$$f_s(s_t,a_t),\approx A_{s_t}+B_{a_t},\quad f_r(s_t,a_t)\approx s_t^TQ_{s_t}+a_t^TR_{a_t}$$
다음으로 이는 LQR(Linear-Quadratic Regulator) 문제가 되며 이는 분명히 해결할 수 있습니다.
iLQR의 경우 현재의 솔루션 주변의 모델을 지역으로 근사하고 LQR 문제를 해결하여 솔루션을 업데이트한 후 이를 반복합니다.
DDP(Differential dynamic programming)의 경우, 이는 유사하나 \(f_s\)의 좀더 높은 차수의 확장이라고 보시면 됩니다.
Model Based Reinforcement Learning (MBRL)
This is a summary of MBRL tutorial from ICML-2020.
kargarisaac.github.io
'AI기술설명' 카테고리의 다른 글
| ICML Tutorial on Model-Based Methods in Reinforcement Learning(모델 기반 강화학습) - 3.루프에서의 모델 기반 제어(Model-based control in the loop) (0) | 2025.01.28 |
|---|---|
| AI모델 학습시 Batch Size와 학습 속도의 상관관계 (1) | 2024.08.31 |
| AI로 추상화 그리기: DALL-E 2 vs Midjourney vs StableDiffusion (0) | 2022.08.31 |
| [MLOps] 고급 레이블링, 데이터 증강 및 데이터 전처리(2) (0) | 2022.03.11 |
| [MLOps] 고급 레이블링, 데이터 증강 및 데이터 전처리(1) (0) | 2022.03.10 |




