늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(5-4)] 특성 상호작용( Feature Interaction) 본문
[해석할 수 있는 기계학습(5-4)] 특성 상호작용( Feature Interaction)
Justin T. 2020. 5. 17. 16:41특성값이 예측 모델에서 서로 상호 작용할 때 하나의 특성에 대한 효과는 다른 특성값에 따라 결정되기 때무에 예측값은 항상 특성값의 합으로만 표현되지 않습니다. 아리스토엘레스의 "전체는 부분의 합보다 크다"라는 말은 상호작용의 존재하에 적용되어 있습니다.
특성 상호작용이란 무엇인가?
기계학습 모델이 두 가지 특성을 기반으로 예측을 하는 경우 예측을 네 가지 측면, 즉 상수항, 첫 번째 특성에 대한 측면, 두 번째 특성에 대한 측면, 그리고 두 가지 특성 사이의 상호작용에 대한 측면으로 나누어서 볼 수 있습니다.
두 가지 특성값 사이의 상호작용은 개별 특성값의 효과를 고려한 후 특성값을 변경함으로써 발생하는 예측값의 변화를 나타냅니다.
예를 들어 모델은 집의 크기(큰 경우 및 작은 경우)및 위치(좋거나 나쁘거나)를 특성값으로서 집의 가치를 예측하는 경우 네 가지 가능한 예측값을 나타낼 수 있습니다.
| 위치 | 크기 | 예측값 |
| good | big | 300,000 |
| good | small | 200,000 |
| bad | big | 250,000 |
| bad | small | 150,000 |
모델 예측값을 다음과 같이 3개의 파트로 분류할 수 있습니다.
- 상수(150,000)
- 크기 특성값에 대한 효과(+100,000 if big; +0 if small)
- 위치에 대한 효과(+50,000 if good; +0 if bad)
이러한 분류는 모델의 예측을 충분히 설명합니다. 모델 예측은 크기와 위치에 대한 단일 특성값 효과의 합이기 때문에 상호작용 효과는 존재하지 않습니다. 작은 집을 크게 만들 때, 예측값은 장소에 상관 없이 항상 100,000씩 증가합니다. 또한 좋은 위치와 나쁜 위치 사이의 예측값의 차이는 크기에 상관 없이 50,000이 납니다.
이번에는 상호작용이 존재하는 경우를 살펴보겠습니다.
| 위치 | 크기 | 예측값 |
| good | big | 400,000 |
| good | small | 200,000 |
| bad | big | 250,000 |
| bad | small | 150,000 |
예측표를 다음과 같은 파트로 분류할 수 있습니다.
- 상수(150,000)
- 크기 특성에 대한 효과(+100,000 if big, +0 if small)
- 위치에 대한 효과(+50,000 if good, +0 if bad)
하지만 이 3가지 파트로는 부족한 부분이 발생합니다. 위치가 좋거나 크기가 큰 경우의 경우 위의 파트만으로는 예측값을 나타내는데 문제가 발생하는 것이지요. 이를 위해 다음과 같은 파트가 추가됩니다.
- 집이 크고 좋은 위치에 있는 경우(+100,000)
이 경우 큰 집과 작은 집의 예측 차이가 위치에 따라 다르기 때문에 크기와 위치 간의 상호작용이라 할 수 있습니다.
상효작용 강도를 추정하는 한 가지 방법은 특성값의 상호 작용에 따라 예측 변동의 양을 측정하는 것입니다. 이러한 측정 방법은 Fiedman과 Popescu(2008)가 도입한 H-statistic이라 부릅니다.
이론: Friedman의 H-statistic
여기서 두 가지 경우에 대해 다루고자 합니다. 첫 번째로, 모델에서 두 가지 특성을 확장하는지의 여부와 확장하는 특성이 서로 상호작용하는지의 여부를 알 수 있는 양방향 상호작용 측정값, 두 번째로, 하나의 특성의 확장이 다른 특성과 상호작용하는지 여부와 총 상호작용 측정값에 대한 것입니다. 이론적으로, 임의의 수의 특성값 사이의 상호작용은 측정될 수 있지만, 이 두 가지 경우가 가증 흥미로운 경우입니다.
두 특성이 상호작용하지 않으면 부분의존 함수를 다음과 같이 분류할 수 있습니다.(부분의존도 함수가 0으로 중심을 맞춘다고 가정합니다).
$$PD_{jk}(x_j,x_k)=PD_j(x_j)+PD_k(x_k)$$
\(PD_{jk}(x_j,x_k)\)는 두 특성에 대한 양방향 부분의존 함수이고 \(PD_j(x_j)\)와 \(PD_k(x_k)\)는 단일 특성값의 부분의존 함수를 나타냅니다.
마찬가지로, 한 특성이 어떠한 다른 특성들과 상호작용을 하지 않을 경우, 예측 함수 \(\hat{f}(x)\)를 부분의존 함수의 합으로서 표현하며, 첫 번째 가수는 j에만 의존하고 두 번째 가수는 j를 제외한 모둔 특성값에 의존합니다.
$$\hat{f}(x)=PD_j(x_j)+PD_{-j}(x_{-j})$$
여기서 \(PD_{-j}(x_{-j})\)는 j번째 특성값을 제외한 모든 특성값에 의존하는 부분의존함수입니다.
이러한 분류는 상호작용 없이(특성 j와 k사이, 또는 각각 j와 다른 모든 특성값 사이) 부분의존(또는 전체 에측)함수를 나타냅니다. 다음으로 관찰된 부분의존함수와 상호작용 없이 분류된 함수간의 차이를 측정합니다. 부분의존(두 특성 간의 상호 작용을 측정하기 위해) 또는 전체 함수(하나의 특성과 다른 모든 특성간의 상호작용을 측정하기 위해)의 분산값을 계산합니다. 상호작용(관찰된 PD와 상호작용이 없는 PD의 차이)에 의해 설명된 분산값의 양은 상호작용 강도 통계로 사용됩니다. 상호 작용이 전혀 없는 경우 통계값은 0이고 모든 변동이 1이면 \(PD_{jk}\) 혹은 \(\hat{f}\)이 부분의존함수의 합으로 설명됩니다. 두 특성값 사이의 상호작용 통계는 각 단일 PD함수가 일정하고 예측값에 미치는 영향이 상호작용을 통해서만 발생함을 의미합니다. H-statistic은 1보다 클 수도 있어 해석하기가 더 어렵습니다. 이는 양방향 상호작용의 분산값이 2차원 부분의존도의 분사보다 클 때 발생할 수 있습니다.
수학적으로 특성 j와 k 사이의 상호작용에 대해 Friedman과 Popescu가 제안한 H-statistics은 다음과 같습니다.
$$H^2_{jk}=\sum_{i=1}^n\left[PD_{jk}(x_{j}^{(i)},x_k^{(i)})-PD_j(x_j^{(i)})-PD_k(x_{k}^{(i)})\right]^2/\sum_{i=1}^n{PD}^2_{jk}(x_j^{(i)},x_k^{(i)})$$
특성값 j가 다른 특성값과 상호작용하는지의 여부를 측정할 때도 마찬가지입니다.
$$H^2_{j}=\sum_{i=1}^n\left[\hat{f}(x^{(i)})-PD_j(x_j^{(i)})-PD_{-j}(x_{-j}^{(i)})\right]^2/\sum_{i=1}^n\hat{f}^2(x^{(i)})$$
H-statistic은 모든 데이터 포인트를 반복하고 각 포인트에서 모든 n개의 데이터 포인트에 대한 종속성을 평가해야 하기 때문에 평가하는데 비용이 매우 많이 듭니다. 최악의 경우 양방향 H-statistic (j vs. k)을 계산하기 위한 기계 학습 모델 예측 함수를 \(2n^2\)회 수행해야 하고 총 H-statistic(j vs. all)에 대해서는 \(3n^2\)가 필요합니다. 계산 속도를 높이기 위해 n개의 데이터 포인트에서 샘플링 할 수 있습니다. 이는 부분의존 추정치의 분산을 증가시키는 단점이 있으며 H-statistic을 불안정하게 만읍니다. 따라서 계산 부담을 줄이기 위해 샘플링을 사용하는 경우 충분한 데이터 포인트를 샘를링 해야 합니다.
Firedman과 Popescu는 H-statistic이 0과 유의하게 다른지 여부를 평가하기 위한 테스트 통계를 제안합니다. 귀무 가설(null hypothesis, 두 집단을 대상으로 실험했을 때 각 집단에서 동일한 결과가 나올 것이라는 가설)은 상호작용이 없다는 의미입니다. 귀무 가설을 전제로 상호작용 통계를 생성하려면 특성 j와 k 또는 다른 모든 요소간의 상호작용이 없도록 모델을 조정할 수 있어야 합니다. 모든 유형의 모델에서 가능하지는 않습니다. 따라서 이 테스트는 모델에 구애받지 않고 모델에 따라 다르며 여기서는 다루지 않겠습니다.
상호작용 강도 통계량은 예측이 확률인 경우 분류 설정에 적용될수도 있습니다.
예제
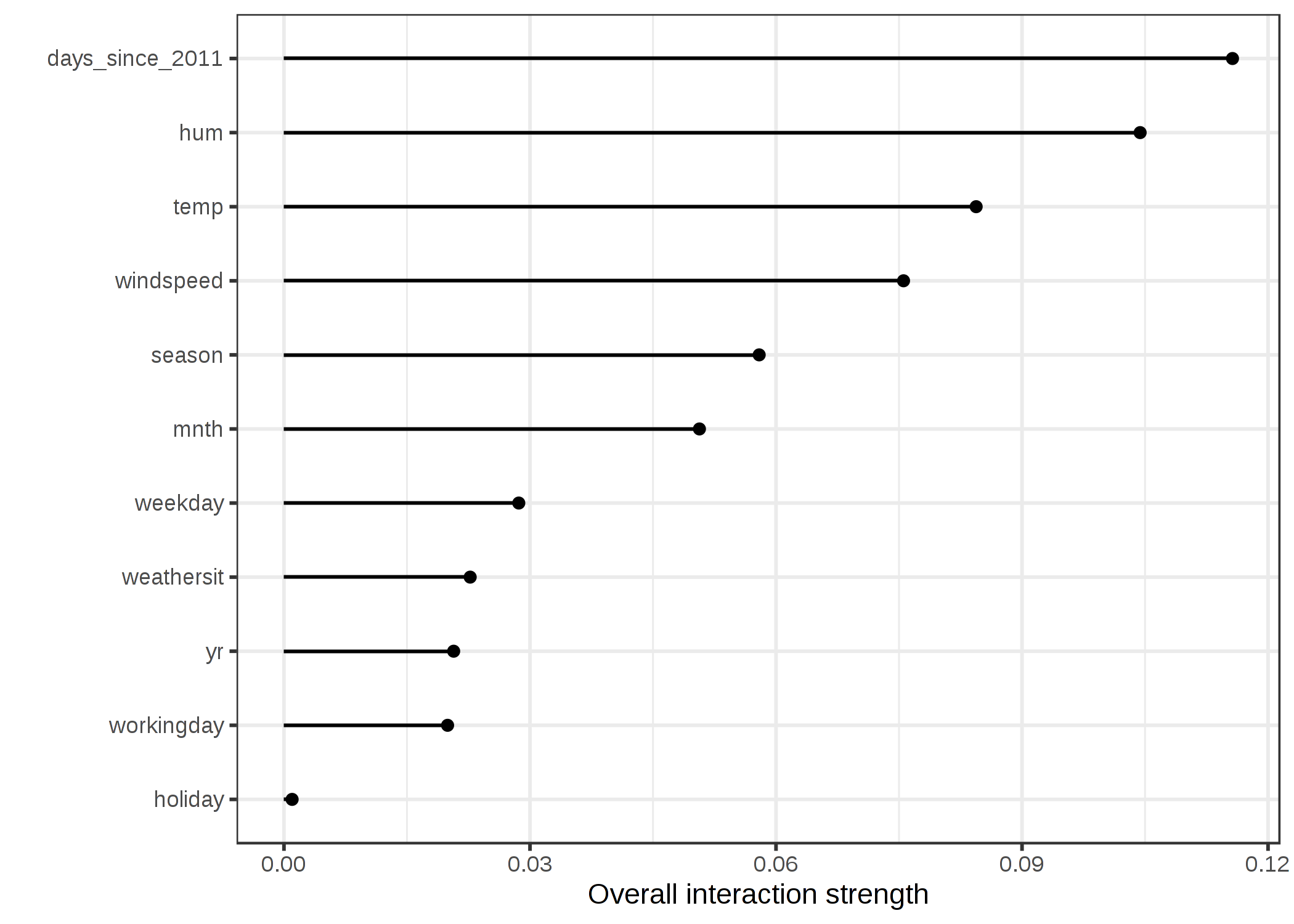
실제로 어떤 특성의 상호작용을 나타낼 수 있는지 살펴보겠습니다. 날씨와 달력 특성을 기준으로 대여 자전거 수를 예측하는 SVM(Support Vector Machine)에서 특성의 상호작용 강도를 측정합니다. 아래 그림은 특성 상호 작용 H-statistic을 나타냅니다.
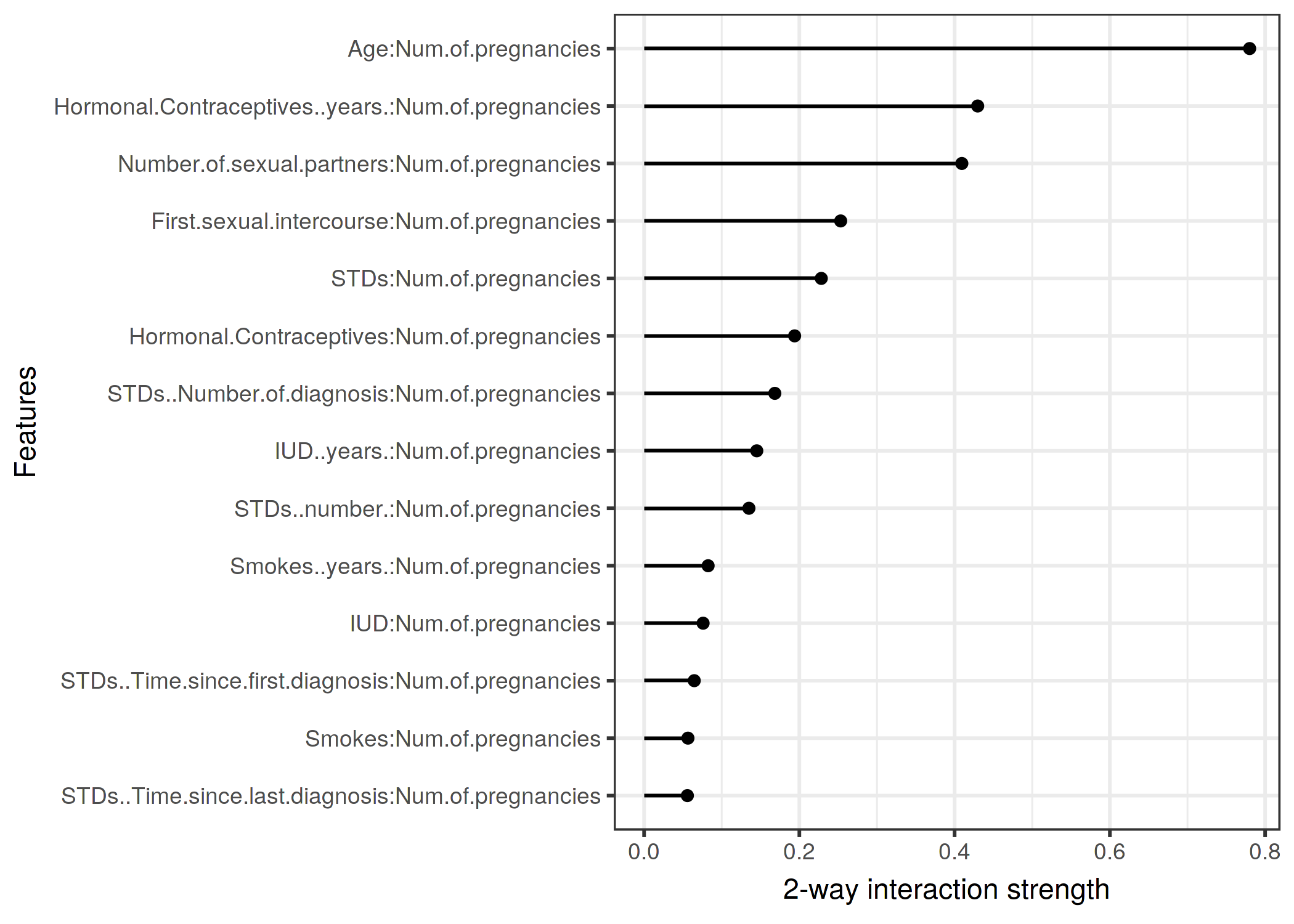
다음 예제에서는 분류 문제에 대한 상호작용 통계를 계산합니다. 몇 가지 위험 요소를 고려하여 자궁 경부함을 예측하도록 학습된 랜덤포레스트에서 특성간의 상호작용을 분석합니다.

다른 모든 특성과 각 특성의 특성 상호작용을 살펴본 후 특성 중 하나를 선택하고 선택한 특성과 다른 특성 간의 모든 양방향 상호작용에 대해 자세하게 알아볼 수 있습니다.
장점
상호작용 H-statistic은 부분의존 분해를 통한 기본 이론을 가지고 있습니다.
H-statistic에는 의미있는 해석이 있습니다. 상호작용은 상호작용에 의해 설명되는 분산값의 비율로 정의됩니다.
통계량은 차원이 없기 때문에 특성과 모델간 비교가 가능합니다.
통계는 특정 형식에 관계없이 모든 종류의 상호작용을 감지합니다.
H-statistic을 사용하면 3개 이상의 특성간의 상호작용 강도와 같은 임의의 더 높은 상호작용을 분석할 수도 있습니다.
단점
첫 번째로 주목할 점으로 상호작용 H-statistic은 계산 비용이 많이 들기 때문에 계산하는데 시간이 오래 걸립니다.
계산에는 주변 분포 추정이 포함됩니다. 모든 데이터 포인트를 사용하지 않을 경우 이러한 추정치에는 특정 차이가 있습니다. 이는 포인트를 샘플링 할 때 추정치가 계산할 때 마다 다르고 결과가 불안정할 수 있음을 의미합니다. 안정적인 결과를 얻기에 충분한 데이터가 있는지 확인하려면 H-statistic에 대한 계산을 몇 번 반복하는 것이 좋습니다.
상호 작용이 0보다 훨씬 큰지의 여부는 확실하지 않습니다. 통계 테스트를 수행해야하지만 이 테스트는 아직 모델 불특정성 버전에서는 사용할 수 있습니다.
테스트 문제와 관련하여 H-statistic이 언제 상호 작용을 "강력한"것으로 간주하기에 충분히 큰지 말씀드리기는 어렵습니다.
또한 H-statistic이 1보다 클 수 있으므로 해석이 어렵습니다.
H-statistic은 상호작용의 강도를 나타내지만 상호작용이 어떻게 다나타는지 알려주지 않습니다. 그것이 부분의존도의 목적입니다. 의미있는 작업흐름도는 상호작용 강도를 측정한 다음 관심있는 상호작용에 대한 2D-부분의존도를 작성하는 것입니다.
입력이 픽셀일 경우 H-statistic을 의미있게 사용할 수 없습니다. 따라시 이 기술은 이미지 분류에 유용하지 않습니다.
상호작용 통계는 특성을 독립적으로 섞을 수 있다는 가정하에 작용합니다. 특성이 서로 밀접환 관련이 있는 경우 이러한 가정이 위반되고 실제로는 거의 불가능한 특성 조합을 통합합니다. 이는 부분의존도와 같은 문제를 갖고 있는 것입니다. 과대 평가 또는 과소 평가로 이어지는경우 일반적으로 말할 수 없습니다.
때때로 결과가 이상하게 나오며 작은 시뮬레이션의 경우 예상되는 결과를 얻어내지 못합니다. 그러나 이는 입증되지 않는 관찰입니다.
구현
여기서 구현된 예는 CRAN에서 iml을 사용할 수 있는 R패키지와 Github의 개발 버전이 사용되었습니다. 특정 모델에 중점을 둔 다른 구현방법이 있습니다. R패키지에서 pre는 RuleFit및 H-statistic을 구현합니다. R패키지 gbm은 그래디언트 부스트 모델과 H-statistic을 구현합니다.
대안
H-statistic이 상호작용을 측정하는 유일한 방법은 아닙니다.
Hooker(2004)의 VIN(Variable Interaction Networks)은 예측 함수를 주효과와 특성 상호작용으로 분해하는 접근 방식입니다. 그 다음 특성 간의 상호작용이 네트워크로 시각화됩니다. 불행히도 아직 이를 사용할 수 있는 소프트웨어는 없습니다.
Greenwell et. al(2018)의 부분의존 기반 특성 상호작용은 두 특성간의 상호작용을 측정합니다. 이 방법은 특정한 하나의 특성값의 특성 중요도(부분의존 함수의 분산으로 정의)를 다른 특성의 서로 다른 고정점에서 조건부로 측정합니다. 분산값이 높으면 특성값들이 서로 상호작용 하고, 0이면 상호작용하지 않습니다. 이에 해당하는 R패키지 vip는 Github에서 사용하실 수 있습니다. 이 패키지는 부분의존도 및 특성 중요도를 다룹니다.
참고자료: https://christophm.github.io/interpretable-ml-book/interaction.html
5.4 Feature Interaction | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 5. 모델 불특정성 방법' 카테고리의 다른 글
| [해석할 수 있는 기계학습(5-6)] 전역 대체모델(Global Surrogate) (0) | 2020.06.17 |
|---|---|
| [해석할 수 있는 기계학습(5-5)] 순열 특성 중요도(Permutation Feature Importance) (0) | 2020.06.15 |
| [해석할 수 있는 기계학습(5-3)] 누적지역효과도( Accumulated Local Effects Plot) (0) | 2020.04.30 |
| [해석할 수 있는 기계학습(5-2)] 개별 조건부 기대치(Individual Conditional Expectation) (0) | 2020.03.23 |
| [해석할 수 있는 기계학습(5-1)] 부분의존도(Partial Dependence Plot) (0) | 2020.03.21 |




