늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(5-8)] 범위 규칙(Anchor) 본문
Anchor는 예측을 충분히 "고정"시키는 의사결정 규칙을 찾아 블랙박스 분류 모델에 대한 개별 예측을 설명합니다. 규칙은 다른 특성값의 변화가 예측에 영향을 미치지 않는 경우 예측을 고정시킵니다. Ancohr는 그래프 검색 알고리즘과 함께 강화 학습 기법을 활용하여 모델 호출 횟수(필요한 실행시간)를 최소로 줄이면서도 지역 최적화에서 회복될 수 있습니다. Ribeiro, Singh, Guestrin은 2018년에 이 알고리즘을 제안하였습다. 이들은 LIME 알고리즘을 도입하였던 분들이기도 합니다.
이전 모델과 마찬가지로 Anchor 접근방식은 미세변동 기반 전략을 배치하여 블랙박스 기계 학습 모델의 예측에 대한 지역 설명을 생성합니다. 그러나 LIME이 사용하는 대리모델 대신 결과적인 설명은 Anchor라 불리는 이해하기 쉬운 IF-THEN 규칙으로 표현됩니다. 이러한 규칙은 범위가 정해져 있기 때문에 다시 활용될 수 있습니다. Anchor는 커버리지 개념을 포함하며, 어떤 다른, 안보일 수 있는 경우에 적용되는지를 정확하게 명시합니다. Anchor를 찾는 일에는 탐색이나 다중 슬롯머신 문제(Multi-armed bandit problem)가 수반되는데, 이는 강화학습의 학습 방법에서 에서 비롯된 것입니다. 이를 위해 설명되고 있는 모든 인스턴스에 대해 이웃, 즉 미세변동이 생성되고 평가됩니다. 그렇게 함으로써 접근방식은 블랙박스의 구조와 내부 매개변수를 무시하여 블랙박스가 관찰되지 않고 변경되지 않은 상태로 유지될 수 있습니다. 따라서 이 알고리즘은 모델 불특성적이며, 어떠한 종류의 모델에도 적용될 수 있다는 것을 의미합니다.
저자들은 논문에서 두 알고리즘을 모두 비교하고 이 알고리즘들이 얼마나 다르게 한 인스턴스의 이웃과 참고하여 결과를 도출하는지를 시각화합니다. 이를 위해 아래 그림은 두 개의 모범 사례를 사용하여 복잡한 이진 분류기(- 또는 +를 예측)를 지역으로 설명하는 LIME과 Anchor 모두를 나타냅니다. LIME의 결과는 LIME이 단지 주어진 미세변동 공간 D 에 가장 근접한 선형 결정 경계를 학습하기 때문에 얼마나 충실한지를 나타내지는 않습니다. 동일한 미세변동 공간을 고려하여 Anchor 접근방식은 모델의 행동에 적용범위를 조정한 설명을 구성하고 경계를 명확하게 표현합니다. 따라서 설계 및 주장에 의해 어떤 경우가 유효한지 정확하게 믿을 수 있습니다. 이러한 속성은 Anchor들을 특히 직관적이고 이해하기 쉽게 만듭니다.

앞에서 언급한 바와 같이 알고리즘의 결과나 설명은 Anchor라고 하는 규칙의 형태로부터 옵니다. 다음의 간단한 예제는 그러한 Anchor을 예시로 합니다. 예를 들어, 타이타닉 침몰 사건에서 승객의 생존 여부를 예측하는 2변수분포 블랙박스 모델이 주어진다고 가정합시다. 이제 우리는 어떻게 모델이 특정 개인에게 생존을 예측하는지 알고자 합니다. Anchor 알고리즘은 아래와 같은 결과 설명을 제공합니다.
| Feature | Value |
| Age | 20 |
| Sex | female |
| Class | first |
| TicketPrice | 300$ |
| More attributes | ... |
| Survived | true |
이에 대한 Anchor의 설명은 다음과 같습니다.
IF SEX = female
AND Class = first
THEN PREDICT Survived = true
WITH PRECISION 97%
AND COVERAGE 15%
이 예는 Anchor가 어떻게 모델의 예측과 근본적인 추론에 필수적인 통찰력을 제공할 수 있는지를 보여줍니다. 그 결과 모델이 어떤 속성을 고려했는가를 보여주는데, 이 경우 여성이라는 성(性)과 일등석(First class)을 말합니다. 인간은 정확성을 위해 가장 중요한 존재로서 이 규칙을 사용하여 모델의 행동을 검증할 수 있습니다. Anchor는 15%의 미세변동 공간 사례에 적용된다는 것을 추가로 알려줍니다. 그러한 경우 설명은 97% 정확하며, 이는 표시된 서술이 예측 결과에 거의 전적인 원인이 있다는 것을 의미합니다.
Anchor A는 다음과 같이 정의됩니다.
$$\mathbb{E}_{\mathcal{D}_x(z|A)}[1_{f(x)=f(z)}]\geq\tau,A(x)=1$$
각 변수들을 설명드리자면
- \(x\)는 설명되는 인스턴스(예: 표 데이터셋의 행 하나)를 나타낸다.
- \(A\)는 \(A\)에 의해 정의된 모든 특성 진술이 \(x\)의 특성값에 해당되는 경우 \(A(x)=1\)과 같은 결과 규칙 또는 Anchors의 집합이다.
- \(f\)는 설명한 분류모델(인공신경망 모델)을 나타낸다. \(x\)와 \(x\)의 미세변동에 대한 Label의 예측에 대해 검색할 수 있다.
- \(D_x (\cdot|A)\)는 \(A\)와 매칭되는 \(x\)의 이웃 분포를 나타낸다.
- \(0 \leq \tau \leq 1\)은 정확도 임계값을 나타낸다. 적어도 \(\tau\)의 지역 충실도를 달성한 규칙만이 유효한 결과로 간주한다.
공식적인 설명은 어려워서 겁먹을 수 있으므로 쉽게 다음과 같이 설명할 수 있습니다.
설명해야 할 인스턴스 \(x\)가 주어진 경우, 규칙이나 Anchor \(A\)가 \(x\)에 적용되면서 \(x\)에 대한 클래스는 동일한 \(A\)가 적용되는 \(x\)의 이웃에 대한 최소 \(τ\)의 일부에 대해 예측된다. 규칙의 정확도는 제공된 기계 학습 모델(지표 함수 \(1_{f(x) = f(z)}\)로 표시)를 사용하여 이웃 또는 미세변동\(D_x (z|A)\)을 평가함으로써 얻는다.
Anchor 찾기
Anchor의 수학적 묘사가 분명하고 간단해 보일 수 있지만, 특정한 규칙을 만드는 것은 어렵습니다. 연속적이거나 커다란 입력 공간에서는 가능하지 않은 모든 \(z \in \mathcal{D}_x(\cdot|A)\)에 대한 \(1_{f(x) = f(z)}\)를 평가하는 것을 요구할 수도 있었습니다. 그러므로, 저자들은 확률론적 정의를 만들기 위해 매개변수 \(0 \leq \delta \leq 1\)를 도입하는 것을 제안합니다.
이러한 방법으로 표본의 정밀도에 관한 통계적 신뢰가 있을 때까지 표본을 추출합니다. 확률론적 정의는 다음과 같습니다.
$$P(prec(A)\geq\tau)\geq{}1-\delta\quad\textrm{with}\quad{}prec(A)=\mathbb{E}_{\mathcal{D}_x(z|A)}[1_{f(x)=f(z)}]$$
위의 두 정의는 적용 범위의 개념에 의해 결합되고 확장됩니다. 그 근거는 모델 입력 공간의 가급적 큰 부분에 적용되는 규칙 발견으로 구성됩니다. 범위는 공식적으로 Anchor의 이웃에 적용될 확률, 즉, Anchor의 변동 공간으로 정의됩니다.
$$cov(A)=\mathbb{E}_{\mathcal{D}_{(z)}[A(z)]}$$
이러한 요소를 포함하면 범위 극대화를 고려한 Anchor의 최종 정의로 이어집니다.
$$\underset{A\:\textrm{s.t.}\;P(prec(A)\geq\tau)\geq{}1-\delta}{\textrm{max}}cov(A)$$
따라서 지금까지의 과정은 모든 합당한 규칙(확률론적 정의가 주어진 정확도 임계값을 만족하는 규칙) 중에서 가장 높은 적용 범위를 가진 규칙을 위해 노력합니다. 이 규칙들은 모델의 더 큰 부분을 설명하기 때문에 더 중요한 것으로 생각됩니다. 진술이 많은 규칙은 진술이 적은 규칙보다 정확도가 높은 경향이 있다는 점에 유의합니다. 특히 \(x\)의 모든 특징을 수정하는 규칙은 평가된 주변 환경을 동일한 인스턴스로 축소합니다. 따라서 모델은 모든 이웃을 동등하게 분류하며, 규칙의 정확도는 1이 됩니다. 동시에 많은 특성을 수정하는 규칙은 지나치게 구체적이며 몇 가지 인스턴스에만 적용됩니다. 따라서 정확도와 범위 사이에는 균형관계에 있다고 할 수 있겠습니다.
Anchor 접근방식은 아래와 같이 네 가지 주요 구성요소를 사용하여 설명을 찾아냅니다.
후보 생성(Candidate Generation)
새로운 설명 후보를 생성합니다. 첫 번째 라운드에서 \(x\)의 특성당 하나의 후보가 만들어지고 가능한 미세변동에 대한 각각의 값을 수정합니다. 다른 라운드마다, 이전 라운드에서 최고의 후보자들은 아직 포함되지 않은 하나의 특성 서술로 확장됩니다.
최우수 후보 등록(Best Candidate Identification)
어떤 규칙이 \(x\)를 가장 잘 설명하는지 후보 규칙을 비교해야 합니다. 이를 위해 현재 관찰된 규칙과 일치하는 미세변동으로 모델을 호출하여 평가합니다. 그러나 이러한 호출은 계산 오버헤드를 제한하기 위해 최소화해야 합니다. 이러한 이유로 이 구성 요소의 핵심에는 순수탐색 다중 슬롯문제(MAB; KL-LUCB)가 있습니다. MAB는 순차적 선택을 사용하여 서로 다른 전략을 효율적으로 탐색하고 이용하기 위해 사용됩니다. 주어진 설정에서 각 후보 룰은 당길 수 있는 슬롯머신으로 봐야 합니다. 슬롯머신을 당길 때마다 각각의 이웃이 평가를 받고, 그에 따라 후보 룰의 보상에 대한 더 많은 정보(Anchor의 경우 정확도)를 얻습니다. 따라서 정확도는 규칙이 설명해야 할 경우를 얼마나 잘 설명하는지를 설명합니다.
후보 정확도 검증(Candidate Precision Validation)
후보가 임계값 \(\tau\)을 초과했다는 통계적 확신이 아직 없는 경우 더 많은 표본을 채취합니다.
수정된 빔 검색(Modified Beam Search)
지금까지의 모든 구성 요소는 그래프 검색 알고리즘이자 너비 우선 알고리즘의 변형인 빔 검색 알고리즘으로 결합됩니다. 이는 각 라운드의 최고 후보 \(B\)를 다음 라운드(\(B\)를 Beam Width라고 부름)로 이동시킨다. 이러한 \(B\)의 최선의 규칙은 새로운 규칙을 만드는 데 사용됩니다. 빔 검색은 각 특성이 규칙에 많아봐야 한 번 포함될 수 있기 때문에 대부분의 \(featureCount(x)\) 라운드에서 수행됩니다. 따라서 매 라운드 \(i\)에서 정확히 \(i\)의 진술을 가진 후보를 생성하고 B를 가장 잘 선택합니다. 따라서 \(B\)를 높게 설정하면 알고리즘이 지역 최적화를 피할 가능성이 높아집니다. 결과적으로, 이는 많은 수의 모델 호출을 필요로 하고 따라서 계산 부하를 증가시키게 됩니다.

이러한 접근방식은 어째서 어떤 시스템이 지금까지 수행하였던 방식으로 인스턴스를 분류했는지에 대한 통계적으로 그럴싸한 정보를 효율적으로 도출하기 위한 완벽해 보이는 방법입니다. 모델의 입력으로 체계적으로 실험하고 각각의 출력을 관찰하여 결론을 내립니다. 이는 제대로 확립되고 연구된 기계 학습 방법(MAB)에 의존하여 모델에 대한 호출 횟수를 줄입니다. 이는 결국 알고리즘의 수행시간을 상당히 줄여줍니다.
복잡도 및 수행시간
Anchor 접근방식의 점근적 런타임 동작을 안다면 특정 문제에 대해 얼마나 잘 수행될 것으로 기대되는지 평가하는 데 도움이 됩니다. \(B\)는 빔 너비를 나타내고 모든 특성의 수를 \(p\)로 표시합니다. 이 경우 Anchor 알고리즘은 다음과 같습니다.
$$\mathcal{O}(B\cdot{}p^2+p^2\cdot\mathcal{O}_{\textrm{MAB}\lbrack{}B\cdot{}p,B\rbrack})$$
이 경계선은 통계적 신뢰도 \(\delta\)와 같은 문제 독립적인 초매개변수(Hyperparameter)로부터 추상화됩니다. 초매개변수를 무시하면 경계선의 복잡도를 줄일 수 있습니다. MAB는 각 라운드에서 \(B \cdot p\) 후보 중에서 \(B\)를 가장 잘 추출하므로, 대부분의 MAB와 그것들의 런타임은 다른 어떤 파라미터보다 \(p^2\) 를 곱합니다.
따라서 알고리즘의 효율성은 특성이 풍부한 문제와 함께 감소한다는 것이 분명해집니다.
표 형식 데이터 예제
표 형식 데이터는 표로 표현되는 구조화된 데이터로, 열(Column)에는 특성과 행 인스턴스가 구현된다. 예를 들어, 자전거 대여 데이터를 사용하여 선택한 인스턴스에 대한 ML 예측을 설명하는 Anchor 접근법의 가능성을 설명합니다. 이를 위해 우리는 회귀를 분류 문제로 전환하고 랜덤 포레스트를 블랙박스 모델로 학습합니다. 대여 자전거 수가 추세선 위인지 아래인지 구분하기 위한 것이지요.
Anchor 설명을 작성하기 전에 미세변동 함수를 정의할 필요가 있습니다. 이를 수행할 쉬운 방법은 예를 들어 학습 데이터에서 표로 된 설명 인스턴스에 직관적인 기본 미세변동 공간을 사용하는 것입니다. 인스턴스에 변동이 발생할 때, 이 기본 접근방식은 Anchor의 진술에 따르는 특성의 값을 유지하는 한편, 고정되지 않은 특성을 지정된 확률로 임의로 샘플링된 다른 인스턴스에서 추출한 값으로 대체합니다. 이 과정은 설명되는 것과 유사하지만 다른 임의의 예로부터 일부 값을 채택한 새로운 예들을 산출합니다. 따라서, 그 결과는 이웃을 닮게 됩니다.

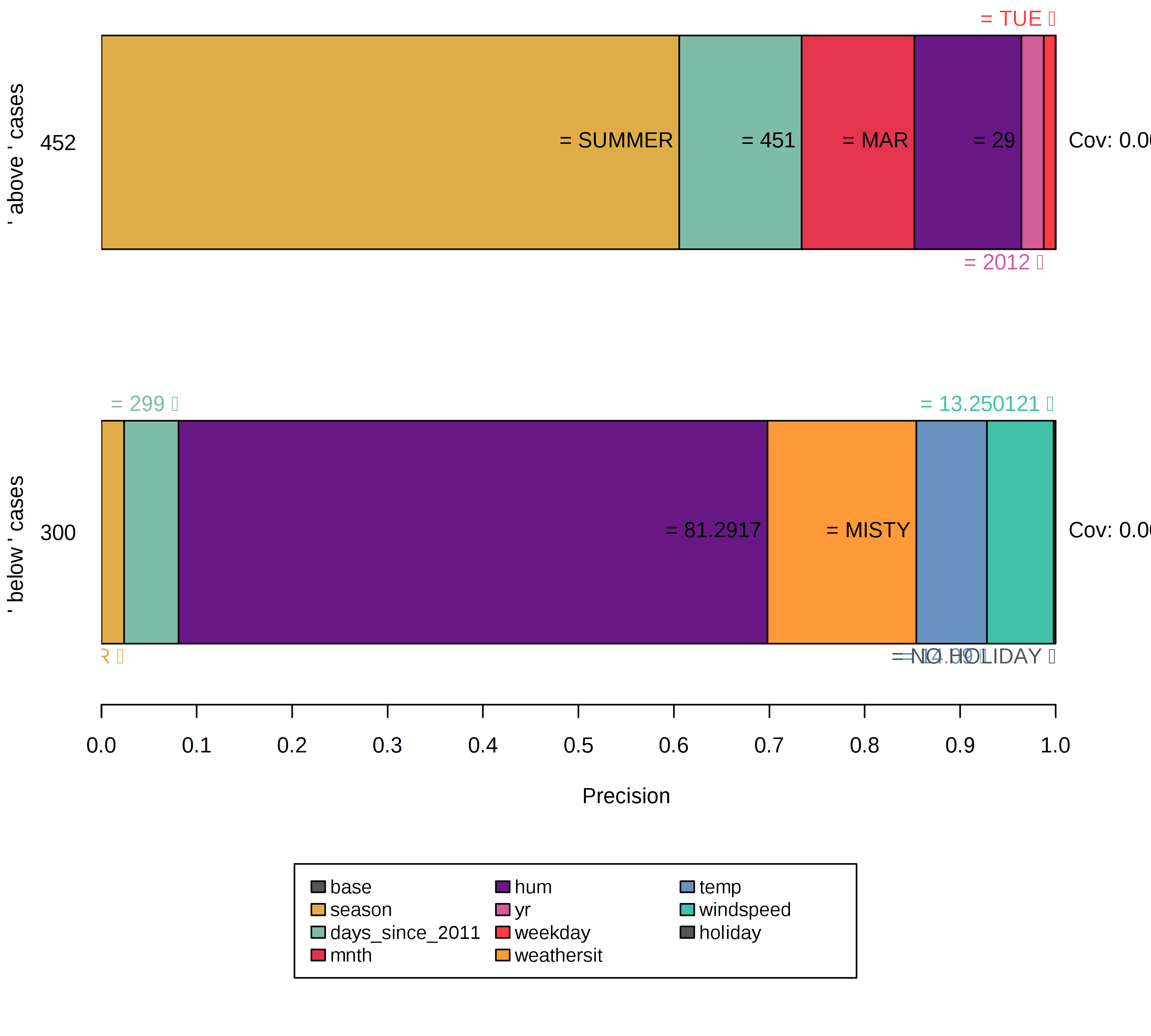
결과는 본능적으로 해석할 수 있고 설명되는 각 인스턴스(instance)에 대해 표시되며, 어떤 특성들이 모델의 예측에 가장 중요한지 알 수 있습니다. Anchor는 근거에 대한 진술이 적기 때문에 범위가 높아 다른 경우에 적용됩니다. 위에 나타낸 규칙은 τ=0.9로 생성되습니다. 따라서 평가된 변동이 Label을 90% 이상 정확하게 지지하고 있는 Anchor에게 요청합니다. 또한 수치적 특성의 표현성과 적용가능성을 높이기 위해 이산화가 사용되었습니다.
이전의 모든 규칙은 모델이 몇 가지 특성을 기반으로 자신 있게 결정하는 인스턴스에 대해 생성되었습니다. 그러나 다른 인스턴스들은 더 많은 특성이 중요하기 때문에 모델에 의해 명확하게 분류되지 않습니다. 이러한 경우 Anchor는 더 구체적이고 더 많은 특성을 구성하며 더 적은 수의 인스턴스에 적용됩니다.
기본 변동 공간을 선택하는 것이 편안한 선택이지만 알고리즘에 큰 영향을 미칠 수 있어 편향된 결과를 초래할 수 있습니다. 예를 들어, 학습세트가 불균형한 경우(각 등급의 동일하지 않은 횟수가 있는 경우), 변동 공간도 마찬가지일 것입니다. 이 조건은 규칙 발견과 그 결과의 정밀도에 더욱 영향을 미치게 됩니다.
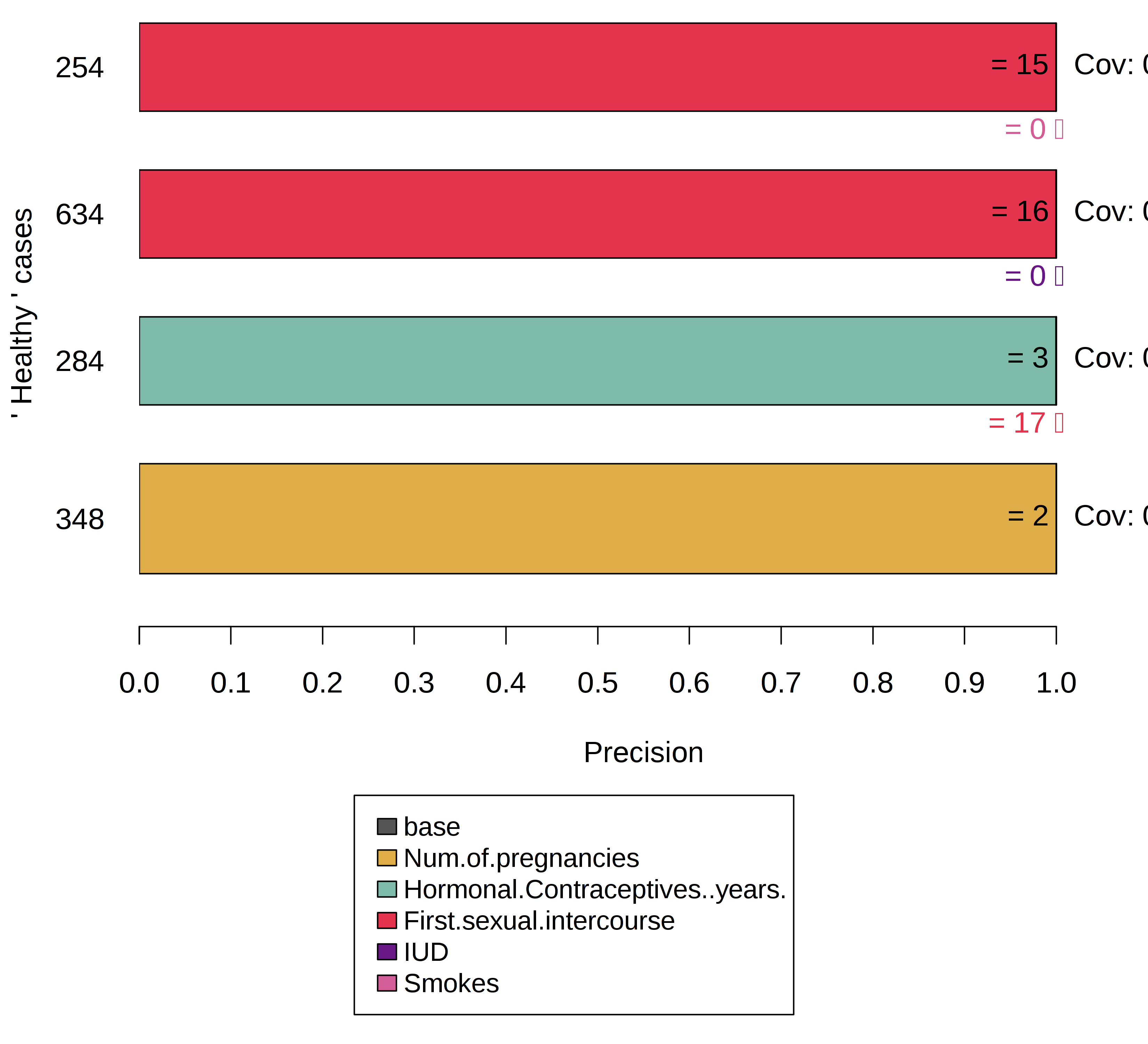
자궁경부암 데이터셋은 이러한 상황의 훌륭한 사례라 할 수 있겠습니다. Anchor 알고리즘을 적용하면 다음 상황 중 하나로 이어지게 됩니다.

이 결과는 원치 않은 결과일 수도 있고 여러 가지 방법으로 접근할 수 있습니다. 예를 들어, 사용자 정의 미세변동 공간은 예를 들어 불균형 데이터 집합 또는 정규 분포와 표본이 다르게 정의될 수 있습니다. 그러나 이는 샘플링된 이웃들이 대표적이지 않고 커버리지 범위를 변경한다는 부작용이 발생합니다. 또는 MAB의 신뢰도 \(\delta\)와 오차 매개변수 값 \(\epsilon\)을 수정할 수 있습니다. 이것은 MAB가 더 많은 표본을 추출하게 할 것이고, 궁극적으로 적은 소수가 더 자주 절대항으로 표본을 추출하게 될 것입니다.
여기서 제시된 예제에서 대부분의 경우 암으로 Label된 자궁경부암 데이터셋의 일부를 사용합니다. 그리고 이에 해당하는 변동 공간을 만들 프레임워크를 갖고 있습니다. 변동은 이제 다양한 예측으로 이어질 가능성이 높으며, Anchor 알고리즘은 중요한 특성을 식별할 수 있습니다. 그럼에도 커버리지의 정의를 고려할 필요가 있습니다. 이는 변동 공간 내에서만 정의됩니다. 앞의 예에서, 우리는 학습 데이터셋을 변동 공간의 기저로 사용했습니다. 여기서 일부 데이터셋만 사용하기 때문에 높은 적용 범위가 반드시 전반적으로 높은 규칙의 중요성을 나타내는 것은 아닙니다.
장점
Anchor 접근방식은 LIME에 비해 여러 가지 장점을 제공합니다다. 먼저, 알고리즘의 결과물은 (일반인에게도) 해석하기 쉬울 정도로 이해하기 쉽습니다.
게다가 Anchor는 부분집합화 하는것이 가능(subsettable)하고 심지어 커버리지 개념을 포함함으로써 중요한 척도를 명시하기도 합니다. 둘째, Anchor 접근법은 모델 예측이 한 인스턴스(instance)의 인접 지역에서 비선형적이거나 복잡한 경우에 동작합니다. 이 접근방식은 대리모델을 피팅(fitting)하는 대신 강화 학습 기법을 배치하기 때문에 이 모델에 적합미달(underfit)할 가능성이 낮습니다.
위에서 말씀드린 것과는 별개로, Anchor 알고리즘은 모델 불특정성(Model-agnostic)이기 때문에 어떤 모델에도 적용하는 것이 가능합니다.
게다가, 배치 샘플링(Batch sampling)을 지원하는 MAB(예: BatchSAR)를 활용하면 병렬화가 가능해 효율성이 높습니다.
단점
Anchor 알고리즘은 대부분의 미세변동 기반의 설명하는자처럼 구성이 가능하고 설정가능성이 강한 설정에 영향을 받습니다. 빔 폭이나 정확도 임계값과 같은 초매개변수는 의미 있는 결과를 산출하도록 조정되어야 할 뿐만 아니라 미세변동 기능도 하나의 영역 및 사용 사례에 대해 명시적으로 설계되어야 합니다다. 표 형식의 데이터가 어떻게 왜곡되는지 생각해 보고, 동일한 개념을 이미지 데이터에 적용하는 방법을 생각해 봅시다(Hint: 이러한 개념은 적용할 수 없습니다). 다행히도 일부 영역(예: 표)에서 기본 접근법을 사용할 수 있어 초기 설명 설정이 가능합니다.
또한, 많은 시나리오에서는 결과가 너무 구체적이고 적용 범위가 낮으며 모델을 이해하는 데 기여하지 않기 때문에 분리가 필요합니다. 이산화(Discretization)하는 것은 도움이 될 수 있지만, 주의깊게 사용하지 않으면 결정의 경계를 흐리게 하여 정반대의 효과를 가져올 수도 있습니다. 최적의 이산화 기법이 없기 때문에 데이터를 어떻게 이산화할 것인지 결정하기 전에 데이터를 인지해야 저조한 결과를 피할 수 있습니다.
Anchor를 건설하려면 모든 미세변동 기반 설명자와 마찬가지로 ML 모델에 대한 많은 호출이 필요합니다. 알고리즘은 호출 수를 최소화하기 위해 MAB를 배치하지만, 여전히 런타임은 모델의 성능에 상당히 많이 좌우되기 때문에 실행시간이 매우 가변적입니다.
끝으로 일부 영역에서는 적용범위의 개념이 정의되지 않습니다. 예를 들어, 한 영상의 슈퍼픽셀이 다른 영상의 슈퍼픽셀과 비교하는 방법에 대한 명확하거나 보편적인 정의는 아직 없습니다.
소프트웨어 및 대안
현재 이용 가능한 소프트웨어로는 Python 패키지(Alibi에 의해 통합됨) 및 Java 두 가지입니다. 전자는 Anchor 알고리즘 저자의 참고논문이고 후자는 본 내용의 예에 사용된 R 인터페이스와 함께 제공되는 고성능 실행프로그램입니다. 현재 Anchor는 표 형식의 데이터만 지원합니다. 그러나 Anchor는 이론적으로 어떤 영역이나 데이터 유형에 대해 구성될 수 있습니다.
참고자료: https://christophm.github.io/interpretable-ml-book/anchors.html
5.8 Scoped Rules (Anchors) | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 5. 모델 불특정성 방법' 카테고리의 다른 글
| [해석할 수 있는 기계학습(5-10)] SHAP (SHapley Additive exPlanations) (1) | 2020.11.30 |
|---|---|
| [해석할 수 있는 기계학습(5-9)] 섀플리값(Shapley Values) (0) | 2020.10.25 |
| [해석할 수 있는 기계학습(5-7)] 지역 대체모델(LIME) (0) | 2020.07.11 |
| [해석할 수 있는 기계학습(5-6)] 전역 대체모델(Global Surrogate) (0) | 2020.06.17 |
| [해석할 수 있는 기계학습(5-5)] 순열 특성 중요도(Permutation Feature Importance) (0) | 2020.06.15 |




