늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(5-9)] 섀플리값(Shapley Values) 본문
예측이 성과물인 게임에서 인스턴스(instance)의 각각의 특징적 가치를 "플레이어"라고 가정함으로써 예측을 설명할 수 있습니다. 협력 게임 이론(Coalitional game theory)의 한 방법인 섀플리 값은 특성들 사이에서 "성과물"을 공평하게 분배하는 방법을 알려줍니다.
일반적인 관점
다음과 같은 경우를 생각해봅시다.
아파트 가격을 예측하는 기계 학습 모델을 교육하셨습니다. 특정 아파트의 경우 30만 유로를 예측하고 이 예측을 설명해야 한다. 이 아파트의 면적은 50㎡이며 2층에 위치하고 있으며 근처에 공원이 있으며 고양이는 금지되어 있다.
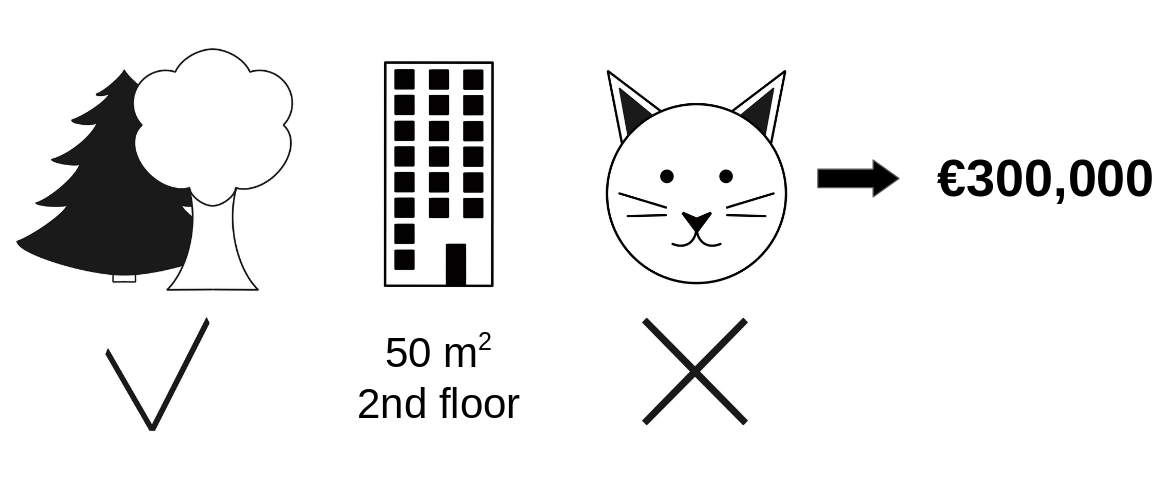
모든 아파트의 평균 전망치는 31만 유로라는 결론을 얻었습니다. 각 특성값이 평균 예측과 비교하여 예측에 얼마나 영향을 주었을까요?
선형 회귀 모형의 경우 설명이 간단합니다. 각 특성의 효과는 특성의 가중치에 특성값을 곱한 값입니다. 이는 모델의 선형성 때문에 효과가 있는 것입니다. 좀 더 복잡한 모델을 설명하기 위해서는 다른 솔루션이 필요합니다. 예를 들어, LIME은 효과를 추정하기 위해 지역 모델을 제안합니다. 또 다른 해결책은 다음과 같은 협력 게임 이론에서 나옵니다. 섀플리(1953)가 만든 섀플리값은 플레이어들에게 전체 성과물에 대한 기여도에 따라 성과물을 배정하는 방식합니다. 플레이어들은 연합에 협력하고, 이 협력으로 일정한 이익을 얻습니다.
플레이어일까? 게임일까? 성과물일까? 기계학습 예측과 해석 가능성과의 연관성은 무엇일까? "게임"은 데이터 집합의 단일 인스턴스에 대한 예측 작업입니다. "이득"은 이 경우에 대한 실제 예측에서 모든 인스턴스에 대한 평균 예측을 뺀 값입니다. "플레이어"는 이득을 얻기 위해 협력하는 인스턴스의 특성값입니다(= 특정한 값을 예측). 위에서 말씀드린 아파트 예제에서 공원-인근, 고양이-금지, 면적-50㎡, 층-2층과 같은 특성값들은 30만 유로의 예측을 얻기 위해 같이 동작합니다. 우리의 목표는 실제 예측(300,000유로)과 평균 예측(310,000유로)이 -10,000유로의 차이가 발생함을 설명하는 것입니다.
이에 대한 답은 다음과 같습니다.
-
공원-인근: 30,000유로
-
면적-50㎡: 10,000유로
-
층-2층: 0유로
-
고양이-금지 -50,000유로
다음과 같은 요소들을 모두 반영해보면 집값이 마이너스가 됨을 알 수 있습니다.
어떻게 우리는 하나의 특성으로부터 섀플리값을 계산할 수 있을까?
섀플리 값은 가능한 모든 조합에 걸쳐 특성값의 평균 여분 기여도(Marginal Contribution)를 나타냅니다. 과연 이것만으로 모든 것이 설명될까요?
아래의 그림에서 공원-인근과 면적-50의 기여에 추가되었을 때 고양이-금지 특성값의 기여도를 평가합니다. 데이터에서 무작위로 다른 아파트 조건을 구성하고 그 가치를 특성에 사용함으로써 단지 공원-인근, 고양이-금지 및 면적-50만이 연립하고 있다는 것을 시뮬레이션합니다.
층-2 값은 무작위로 구성된 층-1로 대체되었습니다. 그런 다음 이 조합으로 아파트 가격을 예측합니다(31만유로). 두 번째 단계에서는 임의로 구성된 아파트에서 고양이 허용/금지 특성의 무작위값으로 대체하여 연합에서 고양이-금지를 제외시킵니다. 이 예제에서 아파트는 고양이-허용이었지만, 다시 고양이-금지로 바뀔 수 있습니다. 우리는 공원-인근과 면적-50의 결합에 대한 아파트 가격을 예측합니다(32만 유로). 고양이-금지의 기여도는 €310000 - €320,000 = -€10.000이었습니다. 이 추정치는 임의로 만들어진 아파트 가격에서 고양이 및 층수 특성 값에 대한 "기부자" 역할을 한 값에 따라 달라집니다. 이 샘플링 단계를 반복해서 기여도를 평균으로 나타낸다면 더 나은 예측을 얻을 수 있을 것입니다.
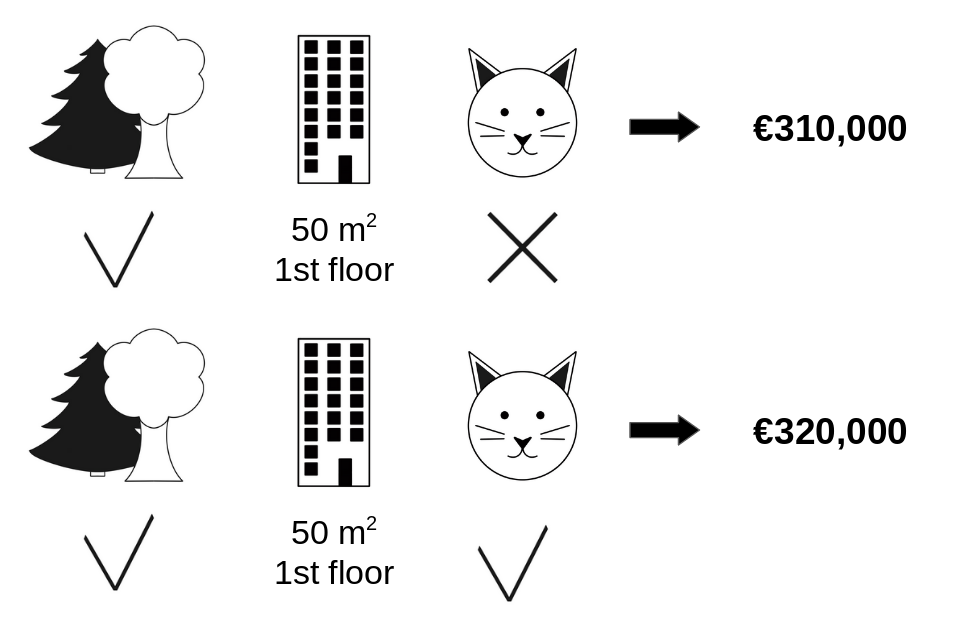
우리는 가능한 모든 연합을 위해 이 계산을 반복합니다. 섀플리값은 가능한 모든 결합에 대한 모든 여분 기여의 평균입니다. 계산 시간은 특성의 갯수에 따라 기하급수적으로 증가합니다. 계산 시간을 관리 가능한 상태로 유지하는 한 가지 해결책은 가능한 결합의 몇 가지 샘플에 대한 기여도만을 계산하는 것입니다.

위 그림은 고양이-금지에 대한 섀플리값을 결정하는 데 필요한 특성값의 모든 조합을 보여줍니다. 첫 번째 행은 어떤 특성값도 없는 조합을 보여줍니다. 2열, 3열, 4열은 "|"로 구분하여 조합의 규모가 커지는 다른 조합을 보여줍니다. 대체로 다음과 같은 조합이 가능합니다.
-
특성값 없음
-
공원-주변
-
면적-50
-
층-2
-
공원-주변 + 면적-50
-
공원-주변 + 층-2
-
면적-50 + 층-2
-
공원-주변 + 면적-50 + 층-2
이러한 각 조합에 대해 우리는 특성값이 제한되어 있는 경우와 그렇지 않은 경우의 예측 아파트 가격을 계산하고 그 차이를 이용하여 여분 기여도를 얻습니다. 섀플리값은 여분 기여도의 (가중치) 평균입니다. 우리는 기계 학습 모델에서 예측을 얻기 위해 아파트 데이터 집합의 무작위 특성값으로 조합되지 않은 특성의 특성값을 대체합니다.
모든 특성값에 대해 섀플리값을 추정하였을때, 특성값 중에서 예측의 전체 분포(평균을 뺀 값)를 얻을 수 있습니다.
예제 및 해석
특성값 j에 대한 섀플리값의 해석은 다음과 같습니다다. j번째 특성값은 데이터셋에 대한 평균 예측과 비교하여 이 특정 인스턴스(instance)의 예측에 \(\phi_j\)를 기여했습니다.
섀플리값은 (확률을 다루는 경우) 분류와 회귀 모두에 대해 동작합니다.
우리는 섀플리값을 사용하여 자궁경부암을 예측하는 랜덤포레스트 모델의 예측을 분석합니다.
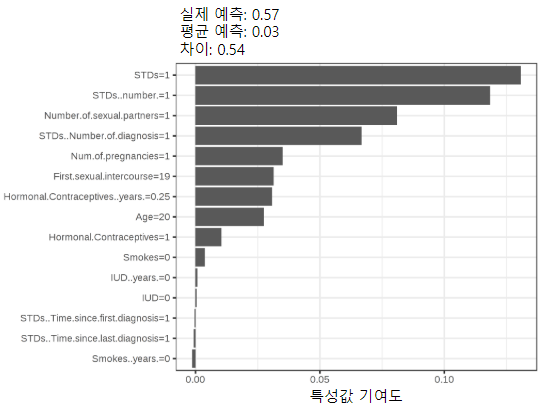
자전거 대여 데이터셋을 위해 날씨와 달력 정보를 고려해 하루 동안 대여된 자전거의 수를 예측하는 랜덤포레스트도 훈련시킵니다. 특정 요일의 랜덤포레스트 예측에 대한 설명은 다음과 같습니다.
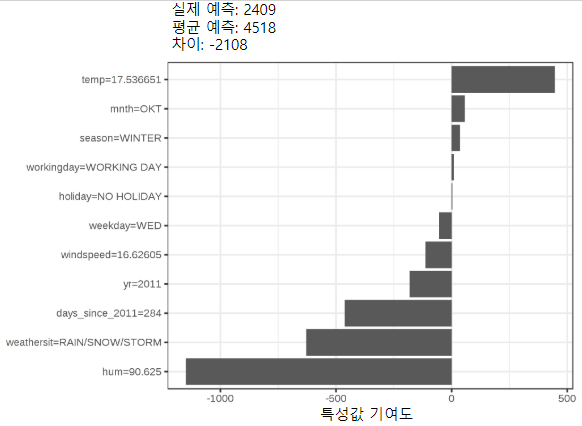
새플리값을 올바르게 해석하도록 주의할 필요가 있습니다. 섀플리값은 다른 조합에서 예측에 대한 특성값의 평균 기여도입니다. 섀플리값은 모델에서 특성값을 언제 제거할 것인지 예측하는 차이가 아닙니다.
좀 더 자세한 섀플리값
이 섹션에서는 호기심 많은 분들을 위한 섀플리값의 정의와 계산에 대해 더 깊이 알아보고자 합니다. 자세한 사항에 관심이 없으실 경우 이 섹션을 건너뛰고 "장점및 단점"으로 넘어가셔도 좋습니다.
각 특성이 데이터 포인트 예측에 어떤 영향을 미치는지 알아봅시다. 선형 모델에서는 각 포인트의 효과를 계산하기가 쉽습니다. 하나의 데이터 인스턴스에 대한 선형 모델 예측은 다음과 같습니다.
$$\hat{f}(x)=\beta_0+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}$$
여기서 x는 우리가 기여도를 계산하고자 하는 인스턴스 입니다. 각 \(x_j\)는 j가 1,...,p일 때 특성값입니다. \(b_j\)는 특성 j에 대한 가중치입니다.
예측 \(\hat{f}(x)\)일 때 j번째 특성의 기여도 \(\phi_j\)는 다음과 같이 나타냅니다.
$$\phi_j(\hat{f})=\beta_{j}x_j-E(\beta_{j}X_{j})=\beta_{j}x_j-\beta_{j}E(X_{j})$$
여기서 \(E(\beta_jX_{j})\)는 특성 j에 대한 평균 효과 예측을 나타냅니다. 기여도는 특성효과에서 평균효과를 뺀 값입니다. 이제 각각의 특성이 예측에 얼마나 기여하고 있는지 알 수 있게 되었습니다. 한 인스턴스에 대해 모든 특성 기여도를 합하면 결과는 다음과 같습니다.
$$\begin{align*}\sum_{j=1}^{p}\phi_j(\hat{f})=&\sum_{j=1}^p(\beta_{j}x_j-E(\beta_{j}X_{j}))\\=&(\beta_0+\sum_{j=1}^p\beta_{j}x_j)-(\beta_0+\sum_{j=1}^{p}E(\beta_{j}X_{j}))\\=&\hat{f}(x)-E(\hat{f}(X))\end{align*}$$
위 식은 데이터 포인트 x에서 평균 예측값을 뺀 값을 나타냅니다. 특성 기여도는 음수일 수 있습니다.
어떤 모델이든 위와 같이 똑같이 할 수 있을까 하는 의문이 생깁니다. 이것을 모델 불특정성 도구로 사용하면 좋을듯 합니다. 보통 다른 종류의 모델에서는 비슷한 가중치를 가지고 있지 않기 때문에, 다른 솔루션이 필요합니다.
이에 대한 힌트는 예상치 못하게도 협력 게임 이론(Cooperative game theroy)에서 알 수 있습니다. 섀플리값은 모든 머신러닝 모델에 대한 단일 예측을 위한 특성 기여도를 계산하기 위한 솔루션입니다.
섀플리값
섀플리값은 집합 S에서 플레이어의 가치 함수 val을 통해 정의됩니다.
특성값의 섀플리값은 가능한 모든 특성값 조합에 대한 결과값, 가중치 및 합계에 대한 기여도입니다.
$$\phi_j(val)=\sum_{S\subseteq\{x_{1},\ldots,x_{p}\}\setminus\{x_j\}}\frac{|S|!\left(p-|S|-1\right)!}{p!}\left(val\left(S\cup\{x_j\}\right)-val(S)\right)$$
여기서 S는 모델 내에 사용된 특성의 부분집합이고, x는 설명되는 인스턴스 특성값과 특성의 갯수 p인 벡터입니다. \(val_x(S)\)는 집합 S에 포함되지 않은 특성에 대해 소외되는 집합 S의 특성값에 대한 예측입니다.
$$val_{x}(S)=\int\hat{f}(x_{1},\ldots,x_{p})d\mathbb{P}_{x\notin{}S}-E_X(\hat{f}(X))$$
S가 포함되지 않은 각 특성에 대해 중적분(Multiple integrations)을 실제 계산해봅니다. 구체적인 예로 기계 학습 모델은 4가지 특성 x1, x2, x3 및 x4로 동작하며 특성값 x1과 x3으로 구성된 집합 S에 대한 예측을 평가합니다.
$$val_{x}(S)=val_{x}(\{x_{1},x_{3}\})=\int_{\mathbb{R}}\int_{\mathbb{R}}\hat{f}(x_{1},X_{2},x_{3},X_{4})d\mathbb{P}_{X_2X_4}-E_X(\hat{f}(X))$$
위 식은 마치 선형 모델의 특성 기여도와 유사하게 보입니다!
"값(value)"이라는 단어의 다양한 적용으로 인해 혼동하지 않으셔도 됩니다. 특성값은 특성 및 인스턴스의 수치값 또는 카테고리값이며, 섀플리값은 예측에 대한 특성 기여도이며, 가치 함수는 플레이어 연합에 대한 지불 함수(특성값)입니다.
섀플리값은 효율(Efficiency), 대칭(Symmetry), 모조(Dummy) 및 부가(Additivity) 특성을 만족하는 유일한 속성 방법이며, 이 두 가지를 합하면 공정한 결과값의 정의로 간주할 수 있습니다.
효율(Efficiency)
특성 기여도는 x와 평균에 대한 예측의 차이를 모두 합해야 합니다.
$$\sum\nolimits_{j=1}^p\phi_j=\hat{f}(x)-E_X(\hat{f}(X))$$
대칭(Symmetry)
두 특성값 j와 k의 기여도가 가능한 모든 결합에 동등하게 기여하는 경우 동일해야 합니다.
집합
$$S\subseteq\{x_{1},\ldots,x_{p}\}\setminus\{x_j,x_k\}$$
위와 같은 조건이 주어질때 만약
$$val(S\cup\{x_j\})=val(S\cup\{x_k\})$$
일 경우 아래와 같은 결과여야 하는 것이지요.
$$\phi_j=\phi_{k}$$
모조(Dummy)
예측값을 변경하지 않는 특성 j는 특성값이 어떤 연대에 추가되든 상관없이 0의 섀플리값을 가져야 합니다.
집합
$$S\subseteq\{x_{1},\ldots,x_{p}\}$$
위와 같 조건이 주어질 때 만약
$$val(S\cup\{x_j\})=val(S)$$
일 경우 다음과 같아야 합니다.
$$\phi_j+\phi_j^{+}$$
부가(Additivity)
결합된 결과값 \(val+val^{+}\)가 있는 게임의 경우 각각의 섀플리값은 다음과 같습니다.
$$\phi_j+\phi_j^{+}$$
랜덤 포레스트를 훈련시켰다고 가정하였을 때, 이는 예측이 많은 의사결정 트리의 평균이라는 것을 알 수 있습니다. 추가(Additivity) 속성은 특성값의 경우 각 트리의 섀플리값을 개별적으로 계산하여 평균화하고 랜덤 포레스트 특성값의 섀플리값을 얻을 수 있음을 보장합니다.
직관(Intuition)
섀플리값을 이해하기 위한 직관적인 방법은 다음과 같습니다.
특성값은 공간에 임의 순서대로 입력됩니다. 공간의 모든 특성값은 게임에 참가합니다(= 예측에 기여합니다). 특성값의 섀플리값은 특성값이 특성값과 결합할 때 이미 공간에 있는 결합이 받는 예측의 평균 변화량을 나타냅니다.
섀플리값 예측
특성값의 가능한 모든 결합(집합)은 정확한 섀플리값을 계산하기 위해 j번째 특성을 포함하거나 포함하지 않고 평가해야 합니다. 몇 가지 특성 개수 이상의 경우, 특성이 추가될수록 가능한 결합의 수가 기하급수적으로 증가함에 따라 이 문제에 대한 정확한 해결책이 문제가 발생합니다. Strumbelj(2014)는 몬테카를로 샘플링에 대한 근사치를 제안하였습니다.
$$\hat{\phi}_{j}=\frac{1}{M}\sum_{m=1}^M\left(\hat{f}(x^{m}_{+j})-\hat{f}(x^{m}_{-j})\right)$$
여기서 \(\hat{f}(x^{m}_{+j})\)는 x에 대한 예측값이지만, 특성 j의 각 값을 제외하고 랜덤 데이터 포인트 z의 특성값으로 대체되는 특성값의 랜덤값입니다. x-벡터 \(x^{m}_{-j}\)은 \(x^{m}_{+j}\)과 거의 동일하지만 \(x_j^{m}\) 값도 샘플 z로부터 취해집니다. 이러한 M의 새로운 각각의 인스턴스들은 두 개의 인스턴스에서 모인 일종의 "프랑켄슈타인 몬스터"입니다.
단일 특성값에 대한 대략적인 Shapley 추정치
- 출력: j번째 특성값에 대한 섀플리값
- 요구사항: 반복 횟수 M, 관심 인스턴스(instance) x, 특성 인덱스 j, 데이터 행렬 X, 기계학습 모델 f
- 모든 m = 1,...,M:
- 데이터 행렬 X에서 랜덤 인스턴스 z 계산
- 특성값의 랜덤 순서 o 선택
- 인스턴스 x 순서: \(x_o=(x_{(1)},\ldots,x_{(j)},\ldots,x_{(p)})\)
- 인스턴스 z 순서: \(z_o=(z_{(1)},\ldots,z_{(j)},\ldots,z_{(p)})\)
- 두 개의 새 인스턴스 구현
- 특성 j 포함: \(x_{+j}=(x_{(1)},\ldots,x_{(j-1)},x_{(j)},z_{(j+1)},\ldots,z_{(p)})\)
- 특성 j 미포함: \(x_{-j}=(x_{(1)},\ldots,x_{(j-1)},z_{(j)},z_{(j+1)},\ldots,z_{(p)})\)
- 여분기여도 계산: \(\phi_j^{m}=\hat{f}(x_{+j})-\hat{f}(x_{-j})\)
- 평균으로 Shapley 값 계산: \(\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\)
먼저 인스턴스 x, 특성 j 및 반복 횟수를 선택합니다. 각 반복에 대해 데이터에서 랜덤 인스턴스 z가 선택되고 특성의 랜덤 순서가 생성됩니다. 인스턴스 x와 샘플 z의 값을 결합하여 두 개의 새로운 인스턴스가 생성됩니다. \(x_{+j}\) 인스턴스는 우리가 알아보고자 하는 인스턴스지만 특성 j 앞에 있는 모든 값은 샘플 z의 특성값으로 대체됩니다. 인스턴스\(x_{-j}\)는 \(x_{+j}\)와 동일하지만, 또한 특성 j는 샘플 z에서 특성 j의 값으로 대체된다. 블랙박스와의 예측 차이는 다음과 같이 계산됩니다.
$$\phi_j^{m}=\hat{f}(x^m_{+j})-\hat{f}(x^m_{-j})$$
이러한 모든 차이를 평균으로 나타내어 다음과 같은 결과를 얻습니다.
$$\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}$$
평균은 X의 확률 분포에 의해 암묵적으로 샘플의 가중치를 측정합니다.
모든 섀플리값을 얻으려면 각 특성에 대해 단계를 반복해야 합니다.
장점
예측과 평균 예측의 차이는 인스턴스의 특성값인 섀플리값의 효율 속성에 공평하게 분포되어 있습니다. 이 특성은 섀플리값을 LIME과 같은 다른 방법으로 구별합니다. LIME은 예측이 특성들 사이에 공정하게 분포된다는 것을 보장하지 않습니다. 섀플리값만이 완전한 설명을 전달할 수 있는 유일한 방법일 수 있습니다. 법이 EU의 "설명권"과 같이 설명력을 요구하는 상황에서 섀플리값은 확고한 이론에 기초하고 그 효과를 공정하게 분배하기 때문에 유일하게 법적으로 준수하는 방법이 될 수 있습니다.
섀플리값은 대조적인 설명을 허용합니다. 예측을 전체 데이터 집합의 평균 예측과 비교하는 대신, 부분 집합 또는 단일 데이터 지점과 비교합니다. 이러한 대조는 LIME과 같은 지역 모델은 갖고있지 않습니다.
섀플리값은 확실한 이론을 가진 유일한 설명 방법입니다. 공리, 즉 효율, 대칭, 모조, 부가와 같은 공리는 설명에 합당한 기저를 제공합니다. LIME과 같은 방법은 기계 학습 모델의 선형 동작을 지역적으로 가정하지만, 이것이 왜 적용되는지에 대해서는 이론이 존재하지 않습니다.
예측을 특성값에 의해 플레이되는 게임으로 설명한다는 것은 정말 충격적이라 생각될 수 있습니다.
단점
섀플리값은 많은 연산 시간을 필요로 한다. 실제 문제의 99.9%에서는 대략적인 해결책만이 실현될 수 있습니다. 섀플리값의 정확한 계산은 특성값의 가능한 결합이 2000여개 이상이고 특성의 "부재"는 랜덤 인스턴스를 그려 시뮬레이션해야 하기 때문에 계산적으로 비용이 많이 듭니다. 이는 섀플리값 추정에 대한 분산을 증가시킵니다. 결합의 기하급수적인 수치는 결합을 표본으로 추출하고 반복 M의 수를 제한하여 처리합니다. M을 줄이면 계산 시간은 줄어들지만 섀플리값의 분산이 증가합니다. 반복 M의 횟수에 대해서는 좋은 경험 법칙은 없습니다. M은 섀플리값을 정확하게 추정할 수 있을 만큼 크지만, 합리적인 시간 내에 연산을 완료할 수 있을 만큼 작아야 합니다. 체르노프 경계를 기준으로 M을 선택할 수 있어야 하는데, 기계학습 예측을 위한 섀플리값을 위해 이렇게 하는 것에 대한 논문은 아직까지 확인되지 않았습니다.
섀플리값은 잘못 해석될 수 있습니다. 특성값의 섀플리값은 모델 훈련에서 특성을 제거한 후의 예측값의 차이가 아닙니다. 섀플리값의 해석은 다음과 같습니다: 현재 특성값 집합을 고려할 때 실제 예측과 평균 예측 사이의 차이에 대한 특성값의 기여도는 추정 섀플리값입니다.
희박한 설명(특성이 거의 없는 설명)을 구한다면 섀플리값은 잘못된 설명 방법이 될 것입니다. 섀플리값 방법으로 만들어진 설명은 항상 모든 특성을 사용합니다. 인간은 LIME에서 생산되는 설명과 같이 선택적인 설명을 선호합니다. LIME은 일반인이 다루어야 하는 설명에 더 나은 선택일 수 있습니다. 또 다른 해결책은 Lundberg 와 Lee(2016)이 도입한 SHAP인데, 섀플리값을 바탕으로 하지만 특성도 거의 없는 설명도 할 수 있습니다.
섀플리값은 특성당 단순한 값을 반환하지만 LIME과 같은 예측 모델은 없습니다. 이는 "만약 내가 연간 300유로를 더 벌게 된다면, 신용 점수는 5점 상승할 것"과 같은 입력 변경에 대한 예측 변동에 대한 진술에 사용할 수 없다는 것을 의미합니다.
또 다른 단점은 새 데이터 인스턴스의 섀플리값을 계산하려면 데이터에 대한 액세스가 필요하다는 것입니다. 관심 인스턴스의 일부를 랜덤하게 그려진 데이터 인스턴스의 값으로 대체할 데이터가 필요하므로 예측 함수에 접근하는 것만으로는 충분하지 않습니다. 이는 실제 데이터 인스턴스처럼 보이지만 학습 데이터에서 실제 인스턴스가 아닌 데이터 인스턴스를 생성할 수 있는 경우에만 피할 수 있습니다.
다른 많은 순열 기반 해석 방법과 마찬가지로 섀플리값 방식도 특성이 관계되는 비현실적인 데이터 인스턴스를 포함하기 때문에 어려움을 겪게 됩니다. 특성값이 결합에서 누락되었음을 시뮬레이션하기 위해 특성을 무시합니다. 이 값은 특성의 여분 분포에서 값을 표본 추출하여 얻습니다. 이는 특성들이 독립적인 한 괜찮습니다. 특성이 종속적인 경우 이 인스턴스에 적합하지 않은 특성값을 샘플링할 수 있습니다. 하지만 이 특성들의 섀플리값을 계산하기 위해 그것들을 사용할 것입니다. 한 가지 해결책은 상관관계가 있는 특성들을 함께 허용하고 그것들에 대해 하나의 상호 섀플리값을 얻는 것일 수 있습니다. 또 다른 적용은 조건부 샘플링입니다. 특성는 같은 팀에 이미 있는 특성을 조건으로 샘플링됩니다. 조건부 표본 추출은 비현실적인 데이터 포인트의 문제를 해결하지만, 새로운 문제가 발생합니다. 결과 값은 Sundariajan (2019)에 의해 밝혀지고 Janzing(2020)가 추가로 논의한 바와 같이 대칭 공리를 위반하기 때문에 더 이상 우리의 게임에 대한 섀플리값이 아니게됩니다.
소프트웨어 및 대안
섀플리값은 iml과 R패키지의 fastshap에 구현되어 있습니다.
섀플리값에 대한 대안적 추정 방법인 SHAP는 다음 포스팅에서 이어서 설명하도록 하겠습니다.
또 다른 접근방식은 breakDown이라고 불리며, breakDown R 패키지에서 구현됩니다. 또한 BreakDown은 예측에 대한 각 특성의 기여도를 보여주지만, 그것들을 단계별로 계산합니다. 이를 게임으로 다시 한 번 비유해 봅시다. 빈 팀부터 시작하여 예측에 가장 크게 기여할 특성값을 추가하고 모든 특성값이 추가될 때까지 반복합니다. 각 특성값이 얼마나 기여하는가는 이미 "팀"에 있는 각각의 특성값들에 따라 달라지는데, 이것은 breakDown 방법의 큰 단점입다. 샤플리값 방법보다 빠르며, 상호작용이 없는 모델의 경우 결과는 동일합니다.
참고자료: christophm.github.io/interpretable-ml-book/shapley.html
5.9 Shapley Values | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 5. 모델 불특정성 방법' 카테고리의 다른 글
| [해석할 수 있는 기계학습(5-10)] SHAP (SHapley Additive exPlanations) (1) | 2020.11.30 |
|---|---|
| [해석할 수 있는 기계학습(5-8)] 범위 규칙(Anchor) (0) | 2020.08.17 |
| [해석할 수 있는 기계학습(5-7)] 지역 대체모델(LIME) (0) | 2020.07.11 |
| [해석할 수 있는 기계학습(5-6)] 전역 대체모델(Global Surrogate) (0) | 2020.06.17 |
| [해석할 수 있는 기계학습(5-5)] 순열 특성 중요도(Permutation Feature Importance) (0) | 2020.06.15 |




