늦깎이 공대생의 인공지능 연구실
[용어정리]Temporal difference learning(시간차 학습) 본문
시간차 학습(Temporal difference learning)이란 무엇인가?
시간차 학습(Temporal difference learning)은 미래에 예상되는 전체 보상을 예측하기 위한 목적으로 사용되며 강화 학습에서 매우 일반적으로 사용되는 비지도 학습 기법입니다. 물론 다른 수치를 예측하는 데도 사용하기도 합니다. 시간차 학습은 기본적으로 주어진 입력값의 미래 값에 종속된 수치를 어떻게 예측할 수 있는지 배우는 방법라 할 수 있습니다. 또한 연속된 중간 보상에서 행동 패턴의 장기적 유용성을 계산하는 데 사용되는 방법이라 할 수 있겠습니다.
기본적으로, 시간차 학습(TD Learning)은 연속 상태에서 변수의 미래 가치를 예측하는 데 중점을 둡니다. 시간차 학습은 보상 예측 문제를 해결하는 데 중요한 돌파구였기도 합니다. 복잡한 추론을 통해 매우 동일한 결과를 생성하는 데 사용될 수 있는 단순한 학습 절차를 대체하기 위한 수학적 기교를 사용한다고 할 수 있습니다.
이 알고리즘이 좋은 성능을 낼 수 있는 비결은 미래의 전체 보상을 계산하기 보다는 다음 순간에 대한 즉각적인 보상값과 자체적으로 예측한 보상값을 조합하는 시도인 것입니다. 지금 순간으로부터 다음 순간 새로운 정보를 가져올 때, 새 예측값은 이전에 예상했던 예측값과 비교합니다. 이 두 예측값이 서로 다른 경우 시간차 학습 알고리즘은 예측값이 서로 얼마나 다른지 계산한 다음 시간차를 이용하여 이전에 예상했던 예측값을 새로운 예측값으로 조정합니다.
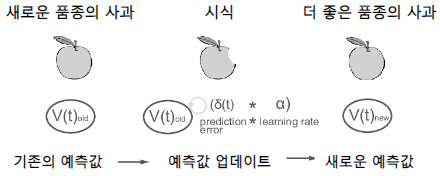
시간차 알고리즘은 항상 기대 예측값과 새로운 예측값을 결합하여 기대값을 실제와 최대한 일치시키고 전체 예측값 체인의 정확도를 점진적으로 높이는 것을 목표로 합니다.
즉, 시간차 학습은 다음 순간에 즉각적인 보상과 자체적인 보상 예측값의 조합하여 예측하는 것을 목표로 합니다.
이러한 TD 학습에서 예측값을 위한 훈련의 결과값은 미래의 예측값입니다. 이 방법은 몬테카를로(Monte-Carlo) 방법과 동적 프로그래밍(DP) 방법의 장점을 조화롭게 합친 것입니다. 몬테카를로 방법은 최종 결과까지 계산한 후에만 추정치를 조정하지만, 시간차 방법은 최종 결과를 명확히 계산하기 훨씬 전에, 이후 더 정확한 미래의 예측값과 일치할 수 있도록 예측값을 조정하는 경향이 있습니다. 이러한 방법은 부트스트래핑(bootstrapping)의 방법 중 하나입니다.
기계 학습의 시간차 학습은 학습 과정을 주도하기 위한 목적으로 연속적인 시간 단계에 대한 예측값의 변화 또는 차이를 사용하는 방식에서 이름이 유래되었습니다.
특정 시간 단계에서의 예측값은 다음 시간 단계에서 동일한 양의 예측에 더 가까워지도록 업데이트됩니다.
시간차 학습(Temporal Differece Learning)에서 사용되는 매개변수는 무엇인가?
시간차 학습에는 주로 3개의 매개변수가 사용됩니다.
- \(\alpha\): 학습율(learning rate)
오차를 기준으로 추정값을 얼마나 조정해야 하는지 정합니다. 이 비율은 0과 1 사이에서 결정됩니다. - \(\gamma\): 할인율(discount rate)
향후 보상이 얼마나 가치 있게 평가되는지를 나타냅니다. 할인율이 클수록 미래 보상의 가치가 더 높게 평가된다는 것을 의미합니다. 할인율도 0과 1 사이에서 결정됩니다. - \(\lambda\): 신뢰할당값(credit assignment variable)
0과 1 사이의 값입니다. 값이 높을수록 이전 상태 및 행동에 더 많은 기여도를 할당할 수 있습니다. - \(\delta\): 값의 변화 또는 차이.
- \(e\): 탐험 대 활용 비율(the ratio reflective of exploration vs. exploitation.)
\(e\)의 확률로 새 옵션을 탐색하는 탐험과 \(1-e\)의 확률로 최대의 보상을 얻을 수 있는 방법을 선택합니다. \(e\)가 클수록 훈련 중에 더 많은 탐험이 수행됨을 의미합니다.
시간차 학습은 신경과학에서 어떻게 사용될까?
1980년대 후반에서 1990년대 초반, 신경과학자들은 도파민 뉴런이 어떻게 행동하는지 이해하려는 시도가 있었습니다. 이 도파민 뉴런들은 주로 중뇌에 모여있지만, 도파민은 뇌의 여러 부분에 투영되며, 전역적으로 관련된 메시지를 잠재적으로 전달합니다. 이 뉴런들의 활성화가 어떤 식으로든 보상과 관련이 있다는 것은 분명했습니다. 그리고, 뉴런의 반응은 또한 감각 입력에 의존했으며 동물들이 특정한 작업에서 더 많은 경험을 얻음에 따라 변화하였습니다.
다행히도, 몇몇 연구원들은 인공지능뿐만 아니라 신경과학의 최근 발전에 대해 긍정적인 생각을 가지고 있었습니다. 그들은 일부 도파민 뉴런의 반응이 보상 예측 오류를 나타낸다는 것을 알게 되었습니다. 뉴런 활성화의 핵심은 어떤 동물이 예상했던 것보다 더 크거나 적은 보상을 받았을 때를 의미합니다.
어떤 동물이 예측된 보상을 받았을 때 도파민 세포의 활성화율은 증가하지 않았지만, 보상이 예상보다 적을 때엔 도파민 세포의 활성화율은 정상 활성화 수준 이하로 떨어졌습니다.
이는 시간차 오류(Temporal Difference Error) 함수가 강화 학습에 사용되는 방식을 매우 가깝게 모방합니다.
연구원들은 이러한 현상을 보고 나서 뇌가 시간차 알고리즘을 사용한다고 제안하였습니다. 즉, 보상값 예측 오류가 계산되고 이 정보가 도파민 신호를 통해 뇌로 전달되는데, 이러한 과정을 통해 시간차 알고리즘이 사용됨으로서 학습을 유도할 수 있게 된 것임을 알게 된 것이지요.
그 후 보상값 예측 오차 이론은 수천 개의 실험에서 광범위하게 테스트되고 검증되었으며, 이후 신경과학에서 가장 성공적인 정량 이론 중 하나로 정립되었습니다.
시간차 모델과 잠재적인 신경 함수 사이의 관계는 행동 연구의 관점에서 설명하기 위해 시간차를 사용하려는 연구를 수행하는 계기가 되었습니다. 기계 학습의 시간차 학습은 정신 분열증이나 도파민의 약리학적 조작이 학습에 미치는 영향과 같은 조건을 연구하고 이해하는 데에도 사용되었습니다.
시간차 학습의 장점은 무엇인가?
- TD 학습 방법은 온라인 또는 오프라인의 각 단계에서 학습할 수 있습니다.
- 이러한 방법은 불완전한 시퀀스에서 학습할 수 있으며, 이는 연속적인 문제에서도 사용될 수 있음을 의미합니다.
- 시간차 학습은 종료되지 않는 환경에서 사용할 수 있습니다.
- TD 학습은 하나의 무작위 행동, 전이, 보상에 의존하기 때문에 몬테카를로 방법보다 분산이 적습니다.
- 몬테카를로 방법보다 더 효율적인 경향이 있습니다.
- 시간차 학습은 마르코프 속성을 이용하여 마르코프 환경에서 더 효과적으로 사용됩니다.
시간차 학습의 단점은 무엇인가?
- 초기값에 대한 민감도가 더 높습니다.
- 편향된 예측을 할 가능성이 있습니다.
시간차 오차(Temporal Difference Error)란 무엇인가?
TD 오차는 강화 학습 전반에 걸쳐 다양한 형태로 발생하며 \(\delta_t=r_t+1+\gamma V(s_{t+1})-V(s_t)\)의 값을 일반적으로 TD 오차라고 합니다. 여기서 TD 오차는 현재의 예측값 \(V_t\)와 할인율이 적용된 예측값 \(V_{t+1}\)의 차이값을 말하며, 실제 보상값은 \(s_t\)와 \(s_{t+1}\) 사이의 전이값으로부터 얻습니다. 매번 TD 오차는 그 때 계산된 오차입니다. 단계 \(t\)에서의 TD 오차는 다음 상태 \(s_{t+1}\)와 다음 보상 \(r_{t+1}\)에 의존하기 때문에 단계 \(t + 1\)까지 사용할 수 없습니다. TD 오차로 가치 함수를 업데이트는 것을 백업이라고 합니다. TD 오차는 벨만 방정식과 관련이 있습니다.
Q러닝과 시간차 학습의 차이점은 무엇인가?
기계 학습의 시간차 학습은 주어진 입력값의 미래 값에 따라 달라지는 값을 예측하는 방법을 배우는 알고리즘입니다. Q러닝은 Q 함수를 학습하는 데 사용되는 특정 TD 알고리즘인 반면, V함수와 Q함수 모두 학습하는 데도 사용될 수 있습니다. V함수만 있는 경우에도 가능한 모든 다음 상태를 반복하고 입력값에 대한 V값이 가장 높은 상태로 이끄는 동작을 선택하여 Q함수를 유도할 수 있습니다.
Model-free RL 개념에서는 상태 전이 함수(모델)를 학습하지 않고 표본에만 의존할 수 있습니다. 그러나 많은 표본을 수집할 수 없어 일부 가상 표본을 생성하여 이를 학습하는 데도 관심을 가질 수 있습니다. 이는, 모델 기반(Model-based) RL에 대한 이야기입니다. 모델 기반 RL은 로봇 및 기계 학습에서 매우 일반적이며, 실제 실험시 로봇 손상이 발생할 수 있기 때문에 가상 표본을 사용하는 것입니다.
시간차 학습에서 사용되는 3가지 알고리즘
시간차 학습 알고리즘에서는 주로 TD(0), TD(1), 그리고 TD(λ)의 3가지 알고리즘을 사용합니다. 이 알고리즘을 설명하기에 앞서 다음과 같은 상황이 주어졌다고 가정합니다.

주어진 조건은 항상 상태 'D'에서 시작하고 50%의 확률로 임의의 노드 또는 종료 상태 'A' 또는 'G'에 도달할 때까지 왼쪽 또는 오른쪽으로 이동합니다. 상태 'A'로 끝나면 0의 보상을 받지만, 상태 'G'로 끝나면 1의 보상을 받습니다. 상태 'B'에서 'F'까지는 보상이 없습니다. 이 예제에서 강화 학습을 사용하는 목적은 Model-free 접근 방식을 통해 이러한 각 상태의 값을 정확하게 예측할 수 있는지 확인하는 것입니다.
TD(1) 알고리즘
먼저 TD(1) 알고리즘에 대해 다루어 보겠습니다. TD(1)는 에피소드가 끝날 때 몬테카를로와 동일한 방식으로 값을 업데이트합니다. 그래서 'A'나 'G'에 착륙할 때까지 임의로 왼쪽이나 오른쪽으로 이동하는 랜덤워크로 되돌아갑니다. 에피소드가 끝나면 이전 상태로 업데이트됩니다. 위에서 언급한 것처럼 \(\lambda\) 값이 높을수록 크레딧을 추가로 할당할 수 있으며 이 경우 \(\lambda\)가 1인 경우 극단값입니다. TD(1)과 MC는 일시적인 환경에서만 작동하므로 업데이트를 수행하려면 '결승선'을 설정할 필요가 있습니다.
이제 TD(1) 알고리즘을 설명해 드리도록 하겠습니다.
$$G_t=R_{t+1}+\lambda R_{t+2}+\cdot\cdot\cdot\cdot+\lambda^{T-1}R_T$$
\(G_t\)는 Episode에서 본 할인율이 적용된 모든 보상의 합계입니다. 따라서 주어진 환경을 수행하는 동안 모든 보상을 추적하고 할인(\(\lambda\))과 함께 합산합니다. 주어진 시점(시간, \(t+1\))에서 즉각적인 보상(\(R\))에 미래 보상(\(R_{t+2}\))의 할인(\(\lambda\))을 더한 것과 같습니다. 이후 \(\lambda^{T-1}\)로 더 많이 할인되는 것을 볼 수 있습니다. 따라서 \(\lambda\)=0.2이고 6단계에서 보상을 할인하는 경우 할인값은 0.00032에 해당하는 \(\lambda^{6-1}\))이 됩니다. 단 6번의 단계를 거치면 값이 상당히 작아집니다.
이제 가치 추정치 \(V(S)\)를 업데이트하겠습니다. 시작할 때는 초기 추정치가 정말 좋지 않다는 것을 알아야 합니다. 랜덤 값 또는 모두 0을 사용하여 초기화한 다음 해당 추정치를 업데이트합니다. 무작위 보행 시퀀스의 경우 'B'와 'F' 사이의 모든 상태에 대한 값을 0으로 [0,0,0,0,0,0,1]와 같이 초기화합니다. 최종 상태는 알려진 대로 그대로 두겠습니다. 우리는 최종 상태의 값을 알고 있기 때문에 최종 상태가 아닌 상태의 값만 예측하려고 한다는 것을 명심하시길 바랍니다.
지금까지 에피소드에서 본 할인된 보상의 합계 \(G_t\)를 사용할 것이고 이 값을 이전의 추정치에서 뺄 것입니다. 이를 TD 오차라고 합니다. 업데이트된 예측값에서 이전 예측값을 뺀 것입니다. 그런 다음 \(\alpha\) 항을 곱하여 해당 오차의 업데이트 기준을 조정합니다. 마지막으로 수정된 TD 오차에 이전 추정치 \(V(S_t)\)만 추가하여 업데이트합니다.
$$V(S_t)=V(S_t)+\alpha(G_t-V(S_t))$$
이렇게 해서 첫 번째 에피소드를 마쳤습니다. 랜덤 워크를 1회 수행하고 보상이 누적되었습니다. 그 다음 각 시간 단계에서 이러한 보상을 가져와서 값의 원래 추정치(모두 0)와 비교했습니다. 우리는 차이를 따져보고 이전 예측값을 조정합니다. 그럼 다시 시작해봅시다. 이렇게 해서 우리는 방금 TD(1) 또는 MC 업데이트를 배웠습니다!
TD(0) Algorithm
지금까지 TD(1)에 대해 설명했으니 다음에 설명 드릴 TD(0)가 훨씬 이해하기 쉬울 것입니다. 아래 식의 괄호 안에 있는 유일한 차이점을 살펴보도록 하겠습니다. 할인된 보상의 누적 합계(\(G_t\))를 사용하는 대신 즉시 보상(\(R_{t+1}\))과 한 단계 앞서 추정된 값의 할인값 (\(V(S_{t+1})\)만 살펴봅니다.
$$V(S_t)=V(S_t)+\alpha(R_{t+1}+\gamma V_{t+1}-V(S_t))$$
이것는 TD(0)와 TD(1) 업데이트의 유일한 차이점입니다. 우리는 방금 위 식의 \(G_t\)를 한 단계 앞선 추정치와 맞바꿨습니다.
추정값을 사용하여 추정값을 업데이트할 때 이를 부트스트랩(Bootstrap)이라고 합니다. 이러한 유형의 기법은 전체 에피소드를 보는 것으로부터 추정값 대 추정값으로 추정하기 때문에 TD(1) 또는 MC보다 더 높은 편차를 가집니다. 그러나 분산이 더 낮은 경향이 있습니다. TD(0)의 또 다른 이점은 TD(1)가 할 수 없는 최종 상태가 없는 환경을 학습할 수 있다는 것입니다.
TD(λ) Algorithm
하나의 에피소드 에피소드(\(TD(1)\))가 끝나기 전에 값을 업데이트하고 한 단계 이상 앞서(\(TD(0)\))를 사용하여 값을 예측하려 합니다. 이것이 바로 \(TD(\lambda)\)가 필요한 부분입니다. \(TD(\lambda)\)에는 forward view와 backward view의 두 가지 구현이 있습니다. forward view는 앞의 모든 n-단계를 살펴보고 \(\lambda\)를 사용하여 이러한 미래 추정치를 본질적으로 감쇄시킵니다. 이 포스팅에서 우리는 \(TD(\lambda)\)의 backward view를 살펴볼 것이지만, forward view와 backward view 모두 동일하다는 것이 입증되었습니다. 혹시 관심있으신 분은 Sutton의 증명을 확인해보시길 바랍니다.
\(TD(\lambda)\)의 backward view는 각 단계에서 값을 업데이트합니다. 따라서 에피소드의 각 단계가 끝나면 이전 단계를 모두 업데이트합니다. 문제는 이전의 모든 단계에 대해 어떻게 가중치를 부여할지, 그리고 크레딧을 어떻게 적절하게 부여 햘지 입니다. 정답은 적격 흔적(Eligibility Traces)이라는 것을 사용하는 것입니다. ET는 기본적으로 주어진 상태에 들어가는 빈도와 최근의 횟수를 기록합니다. 이는 우리의 최종 상태와 관련하여 최근에 방문했을때 뿐만 아니라 자주 방문하는 상태에 크레딧을 할당합니다. 람다(\(\lambda\)) 및 감마(\(\gamma\)) 항은 이러한 흔적(Trace)을 감쇄하는 데 사용됩니다.
$$E_0(s)=0$$
$$E_t(s)=\gamma \lambda E_{t-1}(s)+1(s_t=s)$$
이를 직관적으로 생각하면 최종 상태 'G'로 도달하기 위해 'F' 상태에 자주 방문하고 최근에 방문할 것이며 따라서 많은 업데이트를 받을 것이라는 것을 예상할 수 있습니다. 따라서 ET는 TD 오류에 비례하여 'F' 상태에 더 많은 크레딧을 할당합니다. 그러나 상태 'G'에서 종료하는 것과 관련하여 상태 'B'에 자주 방문되지 않으므로 해당 상태의 값은 자주 업데이트되지 않고 초기화된 위치에서 0에 가깝게 유지됩니다. 여기서부터 우리는 우리의 이전 추정치를 지속적으로 업데이트합니다.
$$\delta_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$$
$$V(s)\leftarrow V(s)+\alpha\delta_tE_t(s)$$
요약
지금까지 시간차학습을 쉽게 설명해 보았습니다. 이 글의 핵심은 초기 추정치를 설정하고, 공간을 탐색하고, 탐험을 하면서 이전 추정치를 업데이트하는 것입니다. 강화학습이 어려운 이유는 이를 어디에 적용해야 할지, 어떠한 환경에서 사용하는지, 보상은 어떻게 제대로 설정해야 하는지 따져봐야 하기 때문입니다만, 적어도 여러분께서는 상태 공간의 탐색 방법과 비지도 model-free 접근법을 사용하여 값을 추정하는 방법에 대해 이해하셨으리라 믿습니다.
참고자료:
https://www.engati.com/glossary/temporal-difference-learning
Temporal difference learning (TD Learning) | Engati
Temporal Difference Learning is a learning technique commonly used in reinforcement learning to predict the total reward expected over the future
www.engati.com
Simple Reinforcement Learning: Temporal Difference Learning
So recently I’ve been doing a lot of reading on reinforcement learning and watching David Silver’s Introduction to Reinforcement Learning…
medium.com
'AI용어정리' 카테고리의 다른 글
| [용어 정리]Modeling Power (0) | 2025.11.02 |
|---|---|
| [용어정리]Weight Decay (0) | 2024.12.22 |
| [용어정리]Synchronized Batch Normalization (0) | 2024.02.12 |
| [용어정리]Ground-truth (9) | 2020.02.25 |
| [용어 정리] Hypothesis set(가설집합) (0) | 2019.10.30 |




