늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(4-1)] 선형 회귀 본문
선형 회귀 모델은 특성값(Feature)의 입력과 가중치(Weight)의 곱의 합으로 목표값으로 예측하는 것을 말합니다. 학습된 관계의 선형성은 해석을 쉽게 만들줍니다. 선형 회귀 모델 오랫동안 통계학자와 컴퓨터 과학자들은 물론 상당한 양의 문제를 다다루는 사람들이 주로 사용하는 알고리즘입니다.
선형 모델들은 일부 특성값 x에 대한 회귀 목표값 y의 의존성을 모델로 만들 수 있습니다. 학습된 관계는 선형이고 이는 단일 인스턴스 i로서 다음과 같이 나타낼 수 있습니다.
$$y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon$$
위 식의 결과는 특성값 p개에 가중치를 곱한 합으로 나타냅니다. \(\beta_j\)값들은 계수의 가중치입니다. 첫 번째 가중치값 \(\beta_0\)는 y절편 값으로 특성값을 곱하지 않습니다. \(\epsilon\)은 예측값과 실제값 사이의 오차를 나타냅니다. 이러한 오차는 가우시안 분포(Gaussian distribution)를 따르는 것으로 나타납니다.
최적의 가중치값을 추정하기 위한 다양한 시도들이 있습니다. 정규방정식(Ordinary least square method)은 대개 실제 결과와 추정 결과 사이의 차이에 제곱한 값을 최소화하는 가중치값을 찾는데 사용됩니다. 정규방정식은 아래의 식과 같이 나타냅니다.
$$\hat{\boldsymbol{\beta}}=\arg\!\min_{\beta_0,\ldots,\beta_p}\sum_{i=1}^n\left(y^{(i)}-\left(\beta_0+\sum_{j=1}^p\beta_jx^{(i)}_{j}\right)\right)^{2}$$
선형 회귀 모델의 가장 큰 장점은 선형성이라 할 수 있겠습니다. 선형성은 추정 절차를 단순하게 만들어줍니다. 특히 선형 방정식은 가중치와 같은 모듈 단계에서 이해하기 쉽도록 해석할 수 있게 해줍니다. 선형 모델과 모든 유사한 모델이 의학, 사회학, 심리학, 그밖에 많은 정량적 연구 분야와 같은 학문 분야에서 많이 활용되는 이유들 중 하나이기도 합니다. 예를 들어 의료 분야에서는 환자의 임상 실험 결과를 예측하는 것에 그치지 않고, 약물의 영향을 계량화 하는 동시에 성별, 나이 및 기타 특성을 해석할 수 있는 방법으로 고려될 수 있습니다. 즉, 의료 분야에서도 선형 모델은 매우 중요한 알고리즘입니다.
예측 가중치값은 통계의 신뢰 구간(Confidence intervals)에 따라 나타납니다. 신뢰 구간은 실제 가중치값을 일정 신뢰도로 포함하는 가중치값 추정의 범위입니다. 예를 들어 가중치 2에 대한 95% 신뢰 구간은 1에서 3 사이일 수 있습니다. 이 간격의 해석은 새롭게 뽑아낸 샘플 데이터에서 추정치를 100회 반복해서 얻으면 선형 회귀 모델이 데이터에 대해 좋은 모델임을 감안했을 때 신뢰구간은 100개 중 95개가 실제 가중치값을 포함하게 됩니다.
모델이 "정확한" 모델인지 아닌지의 여부는 데이터의 관계가 선형성(Linearity), 정규성(Normality), 등분산성(Homoscedasticity), 독립성(Independence), 고정된 특성값, 다중공선성(Multicollinearity)이 나타나지 않는지의 여부에 달려 있습니다.
선형성(Linearity)
선형 회귀 모델은 예측을 모델의 선형 조합으로 강제하며, 이는 최대 강도(Greatest strength)와 최대 한계(Greatest limitation) 둘 다 해당됩니다. 선형성은 해석 가능한 모델로 직결됩니다. 선형 효과는 정량화 하기 쉽고 설명이 용이합니다. 이러한 두 가지 효과는 분리하기 쉽습니다. 특성값 상호 작용 혹은 특성값의 비선형 연관성 때문에 목표값에 대해 의구심이 생기신다면 회귀 스플라인(Regression splines)를 사용하거나 추가적인 상호작용 조건을 반영하여 확인해볼 수 있습니다.
정규성(Normality)
특성값을 고려한 목표값의 결과는 정규분포를 따른다고 가정합니다. 만약 그렇지 않을 경우 특성값의 가중치값의 추정 신뢰 구간은 유효하지 않습니다.
등분산성(Homoscedasticity)
오차값의 분산은 전체 특성공간(Feature space)에 걸쳐 일정하다고 가정합니다. 여러분들이 제곱미터를 기본 단위로 주택의 부동산 가치를 예측하고 싶은 상황일때, 예측값의 오차가 주택의 크기에 관계없이 같은 분산값을 갖는다고 생각되는 선형 모델을 얻을 것으로 예측할 것입니다. 그런데 현실에서 이러한 가정이 종종 틀리는 경우가 발생합니다. 주택의 가격이 더 높아지거나 가격 변동이 커질 경우 예상 가격 오차 조건의 분산값이 더 커질수도 있습니다. 선형 회귀 분석 모델의 평균 오차(예측값과 실제 가격의 차이)가 5만원이라고 가정하고 등분산성을 고려하였을 때, 100만원인 주택과 4만원밖에 안되는 주택의 평균 오차가 5만원이라 할 때 집값이 음수여야만 오차의 평균을 맞출 수 있게됩니다. 이러한 가정은 불합리함을 알 수 있습니다.
독립성(Independence)
각 인스턴스(Instance)는 다른 인스턴스와 관계가 없다고 가정합니다. 환자당 여러번의 혈액검사와 같은 반복 측정을 수행할 경우 데이터 포인트는 독립적이지 않습니다. 종속 데이터의 경우 혼합 효과 모델 혹은 GEE(Generalized estimating equation)와 같은 특수 선형 회귀 모델이 필요합니다. "정상" 선형 회귀 모델을 사용할 경우 모델에서 잘못된 결론을 도출할 수도 있습니다.
다중공선성의 부재(Absense of multicollinearity)
상당한 연관성이 있는 특성값은 가중치의 추정값을 망쳐놓기 때문에 이러한 결과는 대개 원하지 않습니다. 두 특성값이 강하게 연관되는 상황에서는 특성값의 영향이 추가되며 그 효과를 귀속시키기 위해 연관된 특성값의 어느 것이 어떤 다른 특성값에 영향을 미치는지 알 수 없기 때문에 가중치를 추정하는 것에 어려움이 발생합니다.
선형회귀 해석
선형회귀 모델의 가중치값 해석은 해당 특성값의 유형에 따라 달라집니다.
-
수치적 특성값
- 수치적 특성값을 한 단위씩 늘리면 가중치의 추정 결과가 달라집니다. 수치적 특성값의 예는 집의 크기입니다.
-
이진 특성값
- 각 인스턴스에 대해 두 가지 가능한 값 중 하나를 사용하는 특성을 말합니다. 예를 들어 "집에 정원이 있다"와 "집에 정원이 없다"와 같이 나타낼 수 있습니다. 이러한 두 가지의 선택에 따라 가중치값은 달라집니다.
-
여러 카테고리를 포함하는 카테고리 특성값
- 가능한 값의 수가 고정된 특성입니다. 예를 들어 집안의 바닥을 선택함에 있어 "카펫", "라미네이트", "파켓"등 다양한 카테고리가 존재합니다. 많은 카테고리를 다루는 해결책은 One-hot 인코딩인데 이는 각 카테고리에 고유한 이진 컬럼(column)이 있다는 것을 뜻합니다. L이라는 이름의 카테고리 특성에서 다양한 선택지들이 있을 때 이중 하나만 선택하면 됩니다.
-
절편값 \(\beta_0\)
- 절편값은 모든 인스턴스에 항상 1인 "변함없는 특성값"에 대한 특성값의 가중치이다. 대부분의 소프트웨어 패키지는 자동으로 이 "1" 특성값을 추가하여 절편값을 추정합니다. 이는 '모든 수치적 특성값이 0이고 카테고리 특성값이 기준 카테고리에 있는 인스턴스의 경우 모델 예측값은 절편값의 가중치값이다'라고 해석할 수 있습니다. 모든 특성값이 0인 인스턴스는 의미가 없기 때문에 절편값 해석은 일반적으로 관련이 없습니다. 해석은 특성값이 표준화되었을 때만 의미가 있습니다(평균 0, 표준편차 1). 그런 다음, 모든 절편값은 모든 특성값이 평균값인 인스턴스의 예측 결과를 반영합니다.
선형회귀 모델의 특성값에 대한 해석은 아래의 방법들을 통해 자동화 할 수 있습니다.
카테고리 특성값의 해석
특성값 \(x_k\)를 기준 카테고리에서 다른 카테고리로 변경하면 다른 모든 특성값이 고정된 경우 \(y\)에 대한 예측값이 \(\beta_k\)만큼 증가합니다.
선형 모델을 해석하기 위한 또다른 중요한 측정수단은 R제곱(결정계수) 측정입니다. R제곱은 목표값 결과의 전체 분산값이 모델에 의해 설명되는지를 알려줍니다. R제곱이 높을수록 모델이 데이터를 더욱 잘 설명할 수 있습니다. R제곱 공식은 다음과 같이 나타냅니다.
$$R^2=1-SSE/SST$$
SSE는 오류값의 제곱합입니다.
$$SSE=\sum_{i=1}^n(y^{(i)}-\hat{y}^{(i)})^2$$
SST는 데이터 분산값의 제곱합입니다.
$$SST=\sum_{i=1}^n(y^{(i)}-\bar{y})^2$$
SSE는 선형 모델을 적합화한 후 분산값이 얼마인지 알려줍니다. 이는 예측값 및 실제 목표값 사이의 제곱 차이로 측정됩니다. SST는 목표값의 총 분산값입니다. R제곱은 선형 모델로 분산값이 얼마인지를 설명할 수 있는지를 보여줍니다. R제곱 범위는 모델이 데이터를 전혀 설명하지 않는 모델의 경우인 0부터 데이터의 모든 분산을 설명하는 모델의 경우인 1 사이의 범위입니다.
R제곱은 목표값에 대한 정보를 전혀 포함하고 있지 않더라도 모델의 특성값의 갯수에 따라 증가하는 문제점이 있습니다. 따라서 모델에 사용된 특성값의 갯수를 설명하는 조정된 R제곱을 사용하는 것이 좋습니다. 이는 아래의 식과 같이 표현할 수 있습니다.
$$\bar{R}^2=R^2-(1-R^2)\frac{p}{n-p-1}$$
여기서 p는 특성값의 갯수이고 n은 인스턴스 갯수입니다.
R제곱이 매우 낮은 모델을 해석하는 것은 의미가 없습니다. 왜냐하면 그러한 모델은 기본적으로 분산값의 많은 부분을 설명하지 못하기 때문입니다. 가중치값에 대한 어떠한 해석도 의미가 없을겁니다.
특성값의 중요성
선형회귀 모델에서 특성값의 중요성은 t-통계량(t-statictic)의 절대값으로 측정할 수 있습니다. t-통계량은 표준 오차에 따라 크기가 조정된 추정 가중치값입니다.
$$t_{\hat{\beta}_j}=\frac{\hat{\beta}_j}{SE(\hat{\beta}_j)}$$
위 식을 살펴보았을 때 특성값의 중요성은 가중치값에 따라 증가합니다. 추정 가중치값의 분산값이 클수록(즉, 정확한 값에 대한 확신이 적을수록) 특성값의 중요성은 작아집니다.
선형회귀 예제
아래의 예제에서는 날씨와 달력 정보를 고려할 때 특정 날짜에 대여된 자전거의 갯수를 예측하기 위해 선형회귀 모델을 사용합니다. 해석을 위해 추정된 회귀 가중치값을 조사합니다. 특성값은 수치값과 카테고리값으로 구성되어 있습니다. 각 특성값에 대해 표는 추정 가중치값(Weight), 추정치의 표준 오차(SE)및 t-통계량의 절대값 |t|을 나타냅니다.
| Weight | SE | |t| | |
| (Intercept) | 2399.4 | 238.3 | 10.1 |
| seasonSUMMER | 899.3 | 122.3 | 7.4 |
| seasonFALL | 138.2 | 161.7 | 0.9 |
| seasonWINTER | 425.6 | 110.8 | 3.8 |
| holidayHOLIDAY | -686.1 | 203.3 | 3.4 |
| workingdayWORKING DAY | 124.9 | 73.3 | 1.7 |
| weathersitMISTY | -379.4 | 87.6 | 4.3 |
| weathersitRAIN/SNOW/STORM | -1901.5 | 223.6 | 8.5 |
| temp | 110.7 | 7.0 | 15.7 |
| hum | -17.4 | 3.2 | 5.5 |
| windspeed | -42.5 | 6.9 | 6.2 |
| days_since_2011 | 4.9 | 0.2 | 28.5 |
수치적 특성값(온도)
온도가 1도 상승하면 다른 모든 특징들이 고정된 상태에서 예상 자전거 대여수가 110.7개 증가합니다.
카테고리 특성값(날씨)
비가 오거나 눈이 오거나 폭풍우가 칠 때 다른 모든 특징들이 변하지 않는다고 가정할 때 자전가의 예상 대여수는 -1901.5보다 낮아집니다. 날씨가 흐릴 때, 다른 모든 특징들이 똑같다는 것을 고려하면, 예상되는 자전거의 수는 좋은 날씨에 비해 -379.4대 더 낮아집니다.
모든 해석은 항상 "다른 모든 특성값들은 동일하게 유지된다"는 전제에서 나옵니다. 선형회귀 모델의 특징으로 나타나는 것입니다. 예측 목표값은 가중치값이 적용된 특성값의 선형 조합입니다. 추정 선형 방정식은 특성값/목표값 공간의 초평면(Hyperplane)입니다(단순한 특성값의 경우 단순한 선으로 나타납니다). 가중치는 각 방향의 초평면 기울기(경사)로 나타냅니다. 장점은 무언가를 더할 때 개별 특성값 효과의 해석을 다른 모든 특성값과 격리시킬 수 있다는 점입니다. 이는 방정식의 모든 특성값 효과들(가중치값과 특성값의 곱)이 +와 결합되기 때문에 가능한 것입니다. 단점은 특성의 결합확률분포(Joint distribution)를 무시한다는 것입니다. 하나의 특성값을 증가시키되 다른 특성값을 변경하지 않는 것은 비현실적이거나 최소한 가능성이 없는 데이터 포인트로 이어질 수 있습니다. 즉, 기존에 있는 집에 방의 갯수를 늘린다고 집이 넓어지는 않는다는 것이지요.
시각적 해석
위에서 나타낸 가중치값을 나타낸 테이블(가중치 및 분산 추정치)은 아래와 같이 시각화 할 수 있습니다.

가중치를 나타낸 위의 그림은 비/눈/폭풍이 예상되는 자전거 대여수에 부정적인 영향을 미친다는 것을 확인할 수 있습니다. 평일 특성값의 가중치는 0에 가깝고 95% 신뢰구간에 포함되어 있어 평일은 통계적으로 대여수에 유의미한 변화를 주지 않음을 의미합니다. 일부 신뢰 구간은 매우 짧고 추정치는 0에 가깝지만, 특성값의 효과는 통계적으로 의미있음을 볼 수 있습니다. 온도라는 요소도 그러한 후보들 중 하나이지요. 이 그림의 문제점은 특성값이 다른 척도로 측정된다는 것입니다. 날씨에서 추정 가중치는 좋은 날씨의 비/폭풍/눈길의 차이를 반영하지만, 기온의 경우 섭씨 1도 증가만을 반영하고 있습니다. 선형 모델을 적합화시키기 전에 특성들을 평균 0에 표준편차 1인 가우시안 분포로 스케일링하여 추정 가중치를 비교하기 적합하도록 만들 수 있습니다.
효과도(Effect Plot)
선형회귀 모델의 가중치에 실제 특성값을 곱하면 더 의미있게 분석할 수 있습니다. 가중치는 특성값의 척도에 따라 달라지며, 예를 들어 사람의 키를 측정하는 특성값이 있고 측정 단위를 미터에서 센티미터로 전환하면 값이 달라지듯이 말입니다. 가중치는 바뀔 것이지만 실제 데이터 효과는 변하지 않을 것입니다. 또한 데이터에서 특성값의 분포를 아는것 또한 중요합니다. 왜냐하면 분산값이 매우 낮다면 거의 모든 인스턴스가 이 특성값에서 유사한 기여를 갖고 있다는 것을 의미하기 때문입니다. 효과도는 가중치와 특성값의 조합이 데이터의 예측에 얼마나 기여하는지 이해하는데 도움이 될 수 있습니다. 먼저 각 특성값의 가중치에 인스턴스의 특성값을 곱한 것은 다음과 같이 나타낼 수 있습니다.
$$\text{effect}_{j}^{(i)}=w_{j}x_{j}^{(i)}$$
위 식은 상자 그림으로 시각화할 수 있습니다. 그림의 상자에는 데이터의 절반에 대한 효과 범위(25%~75%)가 포함되어 있습니다. 상자의 수직선은 median effect, 즉 인스턴스의 50%는 더 낮은 영향을 미치고 나머지 절반은 예측에 더 높은 영향을 미칩니다. 수평선은 \(\pm1.5\text{IQR}/\sqrt{n}\)까지 확장되며, 이때 IQR은 사분위수 범위(Interquartile range, 75% quantile minus 25% quantile)가 됩니다. 카테고리 특성의 효과는 위의 그림과 비교하여 단일 상자 그림으로 요약할 수 있으며, 여기서 각 카테고리별로 자체 행을 갖습니다.

예상 대여 자전거 수에 가장 큰 영향을 주는 요소는 온도 특성값과 일별 특성값으로, 시간이 지남에 따라 자전거 대여의 추세를 포착합니다. 온도는 그것의 예측에 얼마나 영향을 주는지에 대한 광범위한 범위를 갖고 있습니다. 이 데이터셋(2011년 1월 1일)의 첫날은 매우 작은 경향을 보이며, 이 특성값의 추정 가주치는 양의 값(4.93)이기 때문에 각 날짜의 경향 특성값은 0에서 매우 큰 값이 된다. 즉, 효과는 매일 증가하고 데이터셋(2012.12.31)의 마지막날에는 가장 높은 것을 보실 수 있습니다. 음의 가중치를 가진 효과의 경우, 양의 효과가 있는인스턴스는 음의 특성값을 갖는다는 점에 유의해야 합니다. 예를 들어, 풍속의 부정적인 영향이 높은 날들은 높은 풍속을 가진 날들입니다.
각각의 예측에 대한 설명
하나의 인스턴스의 각 특성값이 예측에 얼마나 영향을 주는걸까요? 이는 그 인스턴스에 대한 효과를 계산함으로서 알 수 있습니다. 여기서 인스턴스별 효과의 해석은 각 특성값에 대한 효과의 분포값과 비교하여야만 타당합니다. 자전거 데이터셋에서 6번째 인스턴스에 대한 선형 모델의 여측을 설명해보도록 하겠습니다. 이 인스턴스는 아래와 같은 값으로 구성되어 있습니다.
| Feature | Value |
| season | SPRING |
| yr | 2011 |
| mnth | JAN |
| holiday | NO HOLIDAY |
| weekday | THU |
| workingday | WORKING DAY |
| weathersit | GOOD |
| temp | 1.604356 |
| hum | 51.8261 |
| windspeed | 6.000868 |
| cnt | 1606 |
| days_since_2011 | 5 |
이 인스턴스의 특성값 효과를 얻으려면 특성값을 선형회귀 모델의 해당 가중치로 곱해야 합니다. 특성값 "WORKING DAY"의 "workingday"값의 효과는 124.9입니다. 섭씨 1.6도의 온도에서 그 효과는 177.6입니다. 이러한 개별 효과를 효과도에 교차하여 추가하는데, 이것은 데이터의 효과의 분포도를 보여줍니다. 이는 개별적인 효과와 데이터의 효과의 분포를 비교할 수 있게 해줍니다.
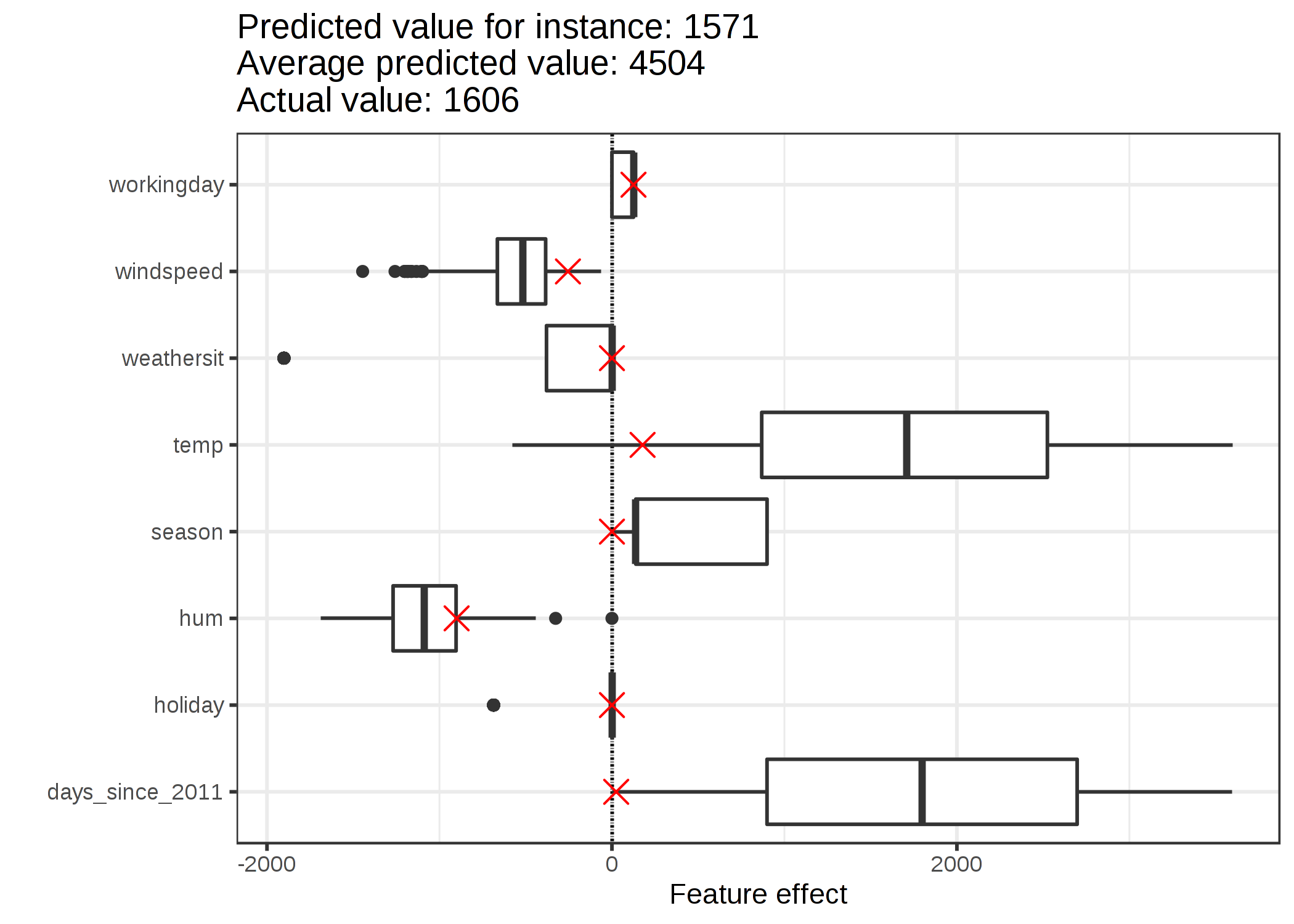
학습 데이터 인스턴스에 대한 예측의 평균을 구하면 평균 4503대를 얻을 수 있습니다. 이에 비해 자전거 대여수는 1571에 불과해 6번째 인스턴스는 작습니다. 효과도는 그 이유를 드러냅니다. 상자 그림은 데이터셋의 모든 인스턴스에 대한 효과의 분포를 보여주며, 교차점은 6번째 인스턴스에 대한 효과를 보여줍니다. 6번째 인스턴스는 다른 대부분의 날에 비해 낮은 2도였기 때문에 낮은 온도 효과를 가지고 있습니다.(우리는 온도 특성값의 가중치가 양수임을 기억해야 합니다). 또한, 2011년 초(5일)의 경우 추세 특성인 "days_since_2011"의 효과는 다른 데이터 인스턴스에 비해 작으며, 추세 특성은 양수 가중치를 갖고 있습니다.
카테고리 특성값의 인코딩(Encoding of Categorical Features)
카테고리 특성값을 인코딩 하는 방법은 여러 가지가 있으며 각각의 방법은 가중치의 해석에 영향을 줍니다.
선형회귀 모델의 기준은 처리 코딩(Treatment coding)이며, 대부분의 경우 충분하다. 서로 다른 인코딩을 사용하는 것은 카테고리 특성을 가진 단일 컬럼(column)에서 다른 (설계)매트릭스를 생성하는 것으로 요약됩니다. 여기서는 세 가지 다른 인코딩을 제시하지만, 더 많은 인코딩 방법들이 있습니다.
우리는 여기서 6개의 인스턴스와 3개의 카테고리를 가진 카테고리 특성값을 가지고 있다고 가정합니다. 처음 두 인스턴스의 경우, 특성값은 카테고리A, 인스턴스 3과 4는 카테고리B, 그리고 마지막 두 인스턴스의 경우 카테고리 C라고 칭합니다.
처리 코딩(Treatment coding)
처리 코딩에서 카테고리당 가중치는 해당 카테고리와 기준 카테고리 사이의 예측값의 추정 차이값입니다. 선형 모델의 절편값은 기준 카테고리의 평균입니다(다른 모든 특성값이 동일하게 유지되는 경우). 행렬의 첫 번째 열은 항상 1인 절편값입니다. 두 번째 열은 i가 카테고리 B에 있는지, 세 번째 열은 카테고리 C에 있는지의 여부를 나타냅니다. 카테고리 A에 대한 열은 필요하지 않습니다. 그러면 선형 방정식이 과적합하게 지정되고 가중치에 대한 고유한 솔루션을 찾을 수 없기 때문입니다. 인스턴스가 카테고리 B나 C에 속하지 않는다는 것을 아는 것만으로 충분합니다.
처리 코딩의 특성값 행렬은 아래와 같이 나타낼 수 있습니다.
$$\begin{pmatrix}1&0&0\\1&0&0\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}$$
이펙트 코딩(Effect coding)
각 카테고리당 가중치는 해당 카테고리에서 전체 평균까지의 추정 y-차이(Estimated y-difference) 입니다(다른 모든 특성값이 0이거나 기준 카테고라기 0인 경우). 첫 번째 열은 절편값을 추정하는 데 사용됩니다. 절편값가 관련된 가중치 \(\beta_0\)은 전체 평균을 나타내고, 2열에 대한 가중치인 \(\beta_1\)은 전체 평균과 카테고리 B의 차이입니다. 카테고리 B의 총 효과는 \(\beta_{0}+\beta_{1}\)입니다. 기준 카테고리 A의 경우 \(-(\beta_{1}+\beta_{2})\)는 전체 평균과의 차이이며, 전체 효과는 \(\beta_{0}-(\beta_{1}+\beta_{2})\)입니다.
이펙트 코딩의 특성값 행렬은 아래와 같이 나타낼 수 있습니다.
$$\begin{pmatrix}1&-1&-1\\1&-1&-1\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}$$
더미 코딩(Dummy coding)
각 카테고리당 \(\beta\)는 각 카테고리에 대한 y의 추정 평균값이다(다른 모든 특성값이 0 또는 기준 카테고리일 경우). 여기서 절편값이 생략되어 선형 모델 가중치에 대한 고유한 솔루션을 찾을 수 있다는 점에 유의합니다.
더미 코딩의 특성값 행렬은 아래와 같이 나타낼 수 있습니다.
$$\begin{pmatrix}1&0&0\\1&0&0\\0&1&0\\0&1&0\\0&0&1\\0&0&1\\\end{pmatrix}$$
과연 선형 모델은 좋은 설명을 만들 수 있을까?
이전 포스팅에서 인간 친화적 설명에서 제시했던 것처럼, 좋은 설명을 구성하는 속성들로만 판단한다면, 안타깝게도 선형 모델은 최선의 설명을 만들어내지 못합니다. 대조적인 이야기지만, 기준 인스턴스는 모든 수치적 특성값이 기준 카테고리에 있는 데이터 포인트입니다. 이는 보통 우리들의 데이터나 현실에서 일어날 것 같이 않은 인위적이고 의미 없는 인스턴스입니다. 하지만 예외가 하나 있습니다. 모든 수치적 특성값이 평균 중심값(특성값에서 특성값의 평균을 뺀 값)이고 모든 카테고리 특성값이 효과 코딩된 경우 기준 인스턴스는 모든 특성값이 평균 특성값을 취하는 데이터 포인트입니다. 이는 존재하지 않는 데이터 포인트 일 수도 있지만 적어도 더욱 가능성이 높거나 더 의미 있는 포인트일 수도 있습니다. 이 경우 가중치에 특성값(feature effects)을 곱하면 "평균 인스턴스"와 대조적으로 예측된 결과에 대한 영향력을 설명합니다. 좋은 설명의 또 다른 측면은 선택성인데, 이는 적은 특성값을 사용하거나 희소 선형모델을 학습시켜 선형 모델을 얻을 수 있습니다. 그러나 기본적으로 선형 모델은 선택적 설명을 만들어내지 않습니다. 선형 방정식이 특성값과 결과 간의 관계에 적합한 모델은 진실한 설명을 만듭니다. 비선형성과 상호 작용이 많을수록 선형 모델의 정확성이 떨어지고 설명의 진실성이 떨어집니다. 선형성은 설명을 더 일반적이고 간단하게 만들어줍니다. 사람들이 관계를 설명하기 위해 선형 모델을 사용하는 주요 요인은 모델의 선형 특성이라 할 수 있습니다.
희소 선형 모형(Sparse Linear Models)
자신이 선택한 선형 모델의 사례들은 모두 멋지고 깔끔해 보입니다. 하지만 실제로는 몇 안되는 특성값만 잇는 것이 아니라 수백, 수천 개의 특성값을 가지고 있을 수도 있습니다. 이를 알게 되었을 때 다시 자신이 선택한 선형 모델은 어때 보이나요? 아마도 자신이 선택한 모델에 대한 해석에 대한 자신감이 떨어질 것입니다. 게다가 인스턴스보다 더 많은 특성값이 있는 상황에서 표준 선형 모델을 전혀 적합하게 만들지 못할 것입니다. 이러한 상황에서 희소성(적은 특성값)을 선형 모델에 도입할 수 있는 방법이 있는 점은 흥미를 갖게 합니다.
라소(Lasso)
라소는 선형회귀 모델에 희소성을 도입하는 자동적이고 편리한 방법입니다. 라소는 "최소 절대 축소 및 선택 연산자"를 의미하며, 선형 회귀 모델에 적용할 경우 선택한 특성값의 가중치의 특성값 선택 및 정규화를 수행햡니다. 가중치를 최적화하는 최소화 문제를 생각해봅니다.
$$min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_i^T\boldsymbol{\beta})^2\right)$$
라소는 이 최적화 식에 다음과 같이 추가합니다.
$$min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_{i}^T\boldsymbol{\beta})^2+\lambda||\boldsymbol{\beta}||_1\right)$$
특성 벡터의 L1-norm인 \(||\boldsymbol{\beta}||_1\)은 거대한 가중치값에 불이익을 줍니다. L1-norm이 사용되기 때문에, 많은 가중치는 0의 추정치를 받고 다른 가중치는 축소됩니다. 매개변수 람다(λ)는 정규화 효과의 강도를 제어하며, 보통 교차 검증(Cross-validation)에 의해 조정됩니다. 특히 람다가 크면 많은 가중치가 0이 됩니다. 특성값의 가중치는 패널티 λ의 함수로 시각화할 수 있습니다. 각 특성값의 가중치는 아래의 곡선과 같이 표시됩니다.

람다 값은 어떻게 설정해야 할까요? 패널티를 튜닝 매개변수로 본다면 교차 검증으로 모델 오류를 최소화 하는 람다를 찾을 수 있습니다. 모델의 해석 가능성을 제어하기 위한 매개변수로 람다를 고려할 수도 있습니다. 패널티가 클수록 모델에 특성값이 더 적어지고(가중치가 0이 되므로)모델을 도 잘 해석할 수 있습니다.
라소 사용 예제
자전거 대여수에 대해 라소를 사용하여 예측해봅니다. 사전에 모델 안에 갖추고자 하는 특성값을 설정합니다. 먼저 2개의 특성을 설정해봅니다.
| Weight | |
| seasunSPRING | 0.00 |
| seasonSUMMER | 0.00 |
| seasonFALL | 0.00 |
| seasonWINTER | 0.00 |
| holidayHOLIDAY | 0.00 |
| workingdayWORKING DAY | 0.00 |
| weathersitMISTY | 0.00 |
| temp | 52.33 |
| hum | 0.00 |
| windspeed | 0.00 |
| days_since_2011 | 2.15 |
라소 path에서 0이 아닌 가중치를 갖는 첫 번째 두 가지 특징은 온도(temp)와 타임 트랜드(days_since_2011)이다.
그렇다면 이번에는 5개의 특성을 설정해봅니다.
| Weight | |
| seasunSPRING | -389.99 |
| seasonSUMMER | 0.00 |
| seasonFALL | 0.00 |
| seasonWINTER | 0.00 |
| holidayHOLIDAY | 0.00 |
| workingdayWORKING DAY | 0.00 |
| weathersitMISTY | -862.27 |
| temp | 85.58 |
| hum | -3.04 |
| windspeed | 0.00 |
| days_since_2011 | 3.82 |
"temp"와 "days_since_2011"의 가중치는 두 가지 특징을 가진 모델과 다르다는 점에 유의합니다. 그 이유는 람다를 줄임으로서 이미 모델 '안'에 있는 특징들 조차 패널티를 덜 받고 더 큰 절대 가중치를 얻을 수 있기 때문입니다. 라소 가중치의 해석은 선형회귀 모델의 가중치 해석에 해당된다. 가중치에 영향을 주기 때문에 특성값이 표준화 되었는지 여부에만 주의를 기울이면 됩니다. 이 사례에서 특성값은 소프트웨어에 의해 표준화 되었지만, 원래 특성값의 척도와 일치하도록 가중치가 자동으로 변환된 것입니다.
선형 모델에서 희소성을 위한 기타 방법
선형 모델에서 특성값의 수를 줄이기 위해 광범위한 스펙트럼을 사용할 수 있습니다.
전처리 방법(Pre-processing methods)
- 수동으로 선택된 특성값(Manually selected features)
전문가의 지식을 사용하여 일부 특성값들을 선택하거나 삭제할 수 있습니다. 가장 큰 단점은 자동화할 수 없고 데이터를 이해하는 사람이 필요하다는 점입니다. - 단일변량 선택(Univariate selection)
단일변량 선택의 예로서 상관 계수를 들 수 있습니다. 특성값과 목표값 사이의 상관관계의 특정 임계값을 초과하는 특성값들만 고려합니다. 단점은 특성값들만 개별적으로 고려한다는 점입니다. 일부 특성값은 선형 모델의 일부 다른 특성값을 설명할 때까지 상관관계를 나타내지 않을 수 있습니다. 단일변량 선택 방법으로는 이러한 것을 놓칠 수 있습니다.
단계별 방법(Step-wise methods)
- 전방 선택(Forward selection)
선형 모델을 하나의 특성값으로 적합화합니다. 각 특성값을 사용하여 작업을 수행합니다. 가장 잘 작동하는 모델(가장 높은 R제곱)을 선택합니다. 그리고 나머지 특성값들에 대해서는 각 특성값을 현재 가장 적합한 모델에 추가하여 다른 버전의 모델을 적합화합니다. 이와 같은 식으로 가장 잘 수행되는 모델을 선택합니다. 모델의 최대 특성값의 수 등 일부 기준에 도달할 때 까지 계속 수행합니다. - 후방 선택(Backward selenction)
전방 선택과 유사한 방법대로 진행됩니다. 그러나 특성값을 추가하는 대신 모든 특성값이 포함된 모델부터 시작하여 어떤 특성값을 제거해야 최고의 성능을 얻을 수 있는지 알아봅니다. 일부 정지 기준에 도달할 때 까지 계속 수행합니다.
장점
가중치의 합계로 예측값을 모델링하면 예측값이 어떻게 생성되는지 투명하게 알 수 있습니다. 그리고 라소를 사용하면 사용되는 특성값의 수가 적은지 확인할 수 있습니다.
많은 사람들이 선형회귀 모델을 사용합니다. 즉, 수많은 곳에서 예측 모델링과 추론을 위해 사용된다는 것을 의미하지요. 선형회귀 모델과 소프트웨어 구현에 관한 교재를 포함하여 높은 수준의 집단 경험과 전문지식들이 있습니다. 선형회귀 분석은 R, Python, Java, Julia, Scala, Javascript등의 프로그래밍 언어에서 사용될 수 있습니다.
수학적으로, 가중치를 추정하는 것이 간단하고 (선형회귀 모델의 모든 가정이 데이터에 의해 충족됨을 가정하였을 때)최적의 가중치를 찾을 수 있음을 보장합니다.
가중치와 함께 신뢰 구간, 테스트, 그리고 확실한 통계 이론을 얻을 수 있습니다. 선형회귀 모델의 확장된 개념들 또한 많이 존재합니다.
단점
선형회귀 분석 모델은 선형 관계, 즉 입력 특성값의 가중치를 곱한 합만 나타낼 수 있습니다. 각각의 비선형성 또는 상호작용은 직접 만들어야 하며 입력 특성값으로 모델에 명시적으로 알아야 합니다.
선형 모델은 또한 종종 예측 성능에 대해 그리 좋지 않습니다. 왜냐하면 배울수 있는 관계는 매우 제한적이고 대개 현실이 얼마나 복잡한지를 지나치게 단순화시키기 때문입니다.
가중치의 해석은 다른 모든 특성값에 따라 달라지기 때문에 직관적이지 않을 수도 있습니다. 결과값 y와 다른 특성값과 상당한 양성의 상관관계가 있는 특성값은 다른 상관 특성을 고려할 때 고차원 공간에서 y와 음성쪽으로 상관관계가 있는 특성값들은 선형 방정식에 대한 득특한 해결책을 찾는 것조차 불가능하게 만듭니다.
예를 들어 여러분은 집의 가치를 예측하는 모델을 가지고 있고 방의 갯수와 집의 평수와 같은 특성값을 가지고 있습니다. 보통 집이 클수록 더 많은 방을 갖고 있기 때문에 집의 크기와 방의 갯수느 매우 밀접하게 연관성이 있습니다. 만약 여러분이 두 가지 특성값을 모두 선형 모델로 받아들인다면 집의 크기가 더 나은 예측 변수이고 큰 양성의 가중치를 갖게 될 수도 있습니다. 한 주택의 크기가 같은 것을 고려할 때, 방의 수를 늘리면 가치가 떨어지거나 상관관계가 나무 강할 때 선형 방정식이 덜 안정적으로 나타날 수 있기 때문에, 방의 갯수는 결국 음성의 가중치를 갖게 될 수도 있습니다.
참고자료: https://christophm.github.io/interpretable-ml-book/limo.html
4.1 Linear Regression | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 4. 해석할 수 있는 모델' 카테고리의 다른 글
| [해석할 수 있는 기계학습(4-6)] 룰핏(RuleFit) (0) | 2020.03.01 |
|---|---|
| [해석할 수 있는 기계학습(4-5)] 의사결정 규칙(Decision Rule) (0) | 2020.02.24 |
| [해석할 수 있는 기계학습(4-4)] 의사결정 트리(Decision Tree) (1) | 2020.01.04 |
| [해석할 수 있는 기계학습(4-3)] GLM, GAM 및 상호작용 (3) | 2019.12.26 |
| [해석할 수 있는 기계학습(4-2)] 로지스틱 회귀 (0) | 2019.12.24 |




