늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(4-3)] GLM, GAM 및 상호작용 본문
선형 회귀 모델의 가장 큰 장점은 예측값이 특성값의 가중치합으로 모델링된다는 것입니다. 또한, 선형 모델은 많은 가정등을 세울 수 있습니다. 그러나 이러한 가정들이 종종 현실에서는 틀릴 경우가 있다는 것입니다. 특성값에 주어진 결과값은 정규분포를 가질 수 있고, 특성값이 상호작용할 수 있으며 특성값과 결과값 사이의 관계가 비선형적일 수도 있습니다. 다행히도 통계학계에서 선형 회귀 모델을 단순한 칼에서 스위스칼로 변형시키는 다양한 수정방법을 개발했다는 것입니다.

이 포스팅에서 다루는 내용을 선형 모델을 확장하기 위한 것이라고 장담하지는 않겠습니다. 여기서는 GLM(Generalized Linear Model)과 GAM(Generalized Additive Models)과 같은 확장 개념에 대한 간단한 소개를 하고자 하며 이는 여러분들께 어느 정도 이해를 위한 도움을 줄 것입니다. 이 내용들을 이해하기 위해 이전에 소개해드린 선형 회귀 모델에 대한 내용을 읽어보시기 바랍니다.
여기서 다시 한 번 선형 회귀 모델의 방정식을 기억해봅니다.
$$y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon$$
선형 회귀 모델은 인스턴스(Instance)의 결과값 y가 가우스 분포에 따르는 개별 오차 ε로 p개의 특성값의 가중치합에 의해 표현될 수 있다고 합시다. 데이터를 이 방정식에 넣음으로서 선형 회귀 모델을 통해 많은 모델 해석력을 얻을 수 있습니다. 특성 효과는 부가적인 것으로, 상호작용이 없음을 의미하며, 관계는 선형적이라고 해석할 수 있습니다. 즉, 한 단위에 의한 특성값의 증가는 예측된 결과의 증가/감소로 직접 해석될 수 있습니다. 선형 모델을 사용하면 특성값과 예상 결과 사이의 관계를 단일 수치, 즉 추정 가중치로 압축할 수 있습니다.
그러나 단순한 가중치합은 수많은 실제 예측 문제에서는 상당히 제한적입니다. 여기서는 고전적인 선형 회귀 모델의 세 가지 문제와 이를 해결하는 방법에 대해 알아보고자 합니다. 가정이 잘못되었을 가능성이 있는 여러 가지 유형의 문제들이 더 있지만, 아래의 그림에 표시된 세 가지 경우에 집중하고자 합니다.
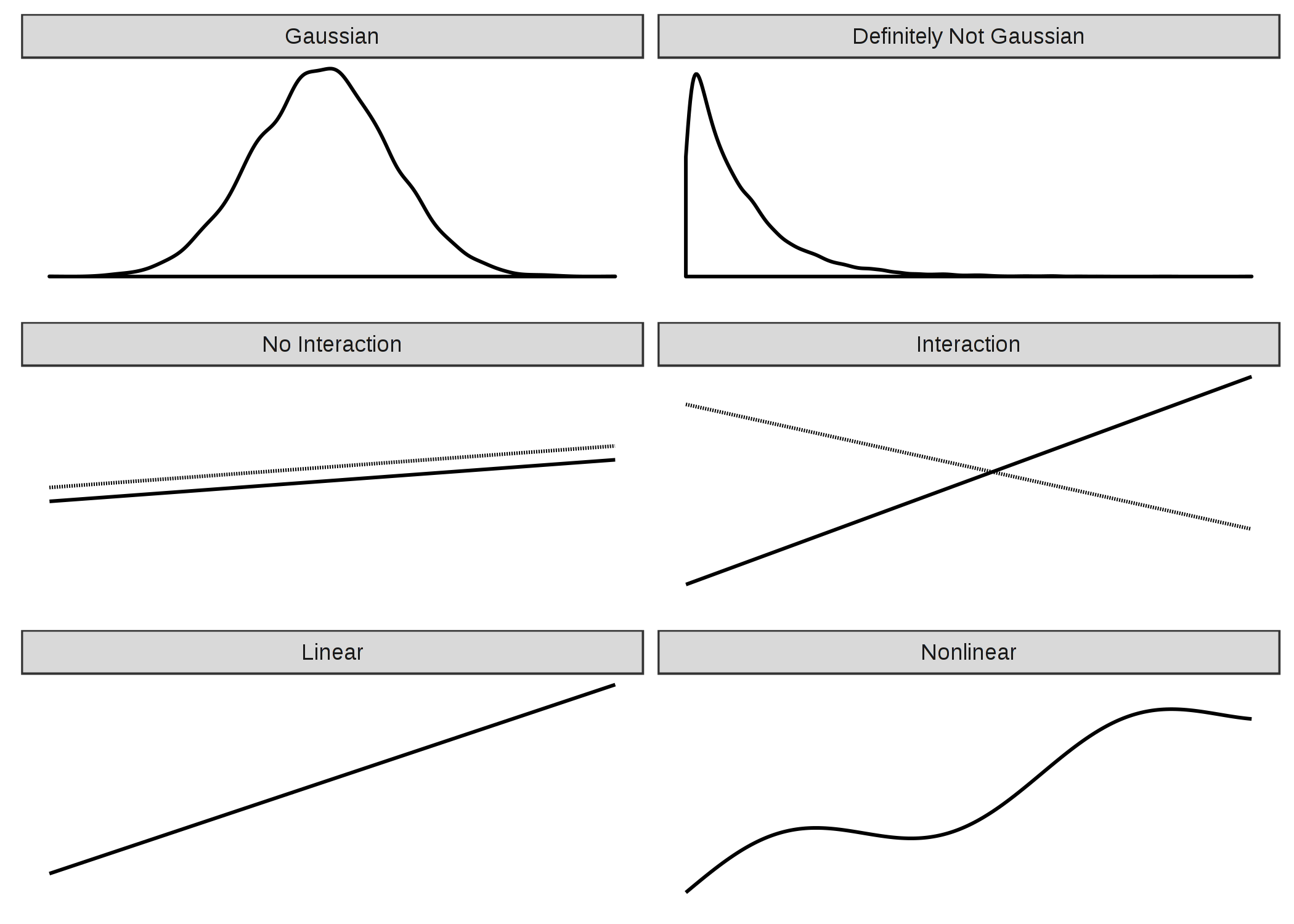
그렇다면 위의 세 가지 문제에 대한 해법을 살펴봅니다.
-특성값에 의한 목표 결과값 y가 정규분포를 따르지 않는 경우
주어진 날짜에 얼마나 많은 시간동안 자전거를 탈지 예측한다고 가정합니다. 특성값으로 날씨 등을 사용한다고 하였을 때 선형 모델을 사용하면 0분 이하의 값을 갖는 정규분포값이 나오기 때문에 마이너스 시간을 예측해버리게 됩니다. 또한 선형 모델로 확률을 예측하려 할 때는 음수 또는 1보다 큰 확률을 얻게 될 수 있습니다.
해결방법: Generalized Linear Models(GLMs)
-특성값이 상호작용(Interaction)하는 경우
평균적으로, 가랑비는 자전거를 타고 가고 싶은 욕구에 약간 부정적인 영향을 줍니다. 그러나 여름 혹은 러시아위 시간대에는 비가 오는 것을 선호할 수도 있습니다. 왜냐하면 날씨가 좋은 날에만 자전거를 타는 사람들은 집에 있을 것이고 자전거 도로에는 자전거를 타는 사람들이 거의 없기 때문입니다. 즉, 시간과 날씨 사이의 상호작용으로 순수 적층 모델로는 이를 포착하기 어렵습니다.
해결방법: 직접 상호작용 추가
-특성값과 y의 실제 관계가 선형이 아닌 경우
0도에서 25도 사이에, 자전거를 타고 싶은 욕구에 미치는 온도의 영향은 선형적일 수 있으나, 이는 0도에서 1도로 증가하면 20도에서 21도로 증가했을 때와 같은 자전거를 타고자 하는 욕구가 증가한다는 것을 의미합니다. 하지만 더 높은 온도에서는 자전거를 타고 싶은 수요가 낮아지게 됩니다.
해결방법: Generalized Additive Models(GAMs); 특성값의 변환
이제 이 세 가지 문제에 대한 해결책을 설명하고자 합니다.
정규분포가 아닌 결과값 - GLMs
선형 회귀 모델은 입력 특성값에 주어진 결과가 정규분포를 따른다고 가정합니다. 이러한 가정은 많은 경우들을 제외합니다. 결과값은 카테고리(암 vs 건강), 개수(출산한 아이의 수), 사건 발생시간(기계가 고장난 시간) 또는 매우 높은 값(가계 소득)이 될 수 있습니다. 선형 회귀 모델은 이러한 모든 유형의 결과를 모델화하기 위해 확장할 수 있습니다. 이러한 확장은 일반화된 선형 모델(Generalized Linear Models) 또는 줄여서 GLM이라 합니다.
GLM의 핵심 개념은 다음과 같습니다.
- 특성값의 가중치합은 유지하되 정규분포가 아닌 결과 분포를 허용하고 이 분포의 예상 평군과 가중치합을 비선형 함수를 통해 연결합니다. 예를 들어, 로지스틱 회귀 모델은 결과에 대한 베르누이 분포(Bernoulli distribution)를 가정하고 로지스틱 함수를 사용하여 예상 평균과 가중치를 연결합니다.
GLM은 결과 유형에 따라 유연하게 선택할 수 있는 연결함수 g를 사용하여 특성값의 가중치합을 가정한 분포의 평균값과 수학적으로 연결합니다.
$$g(E_Y(y|x))=\beta_0+\beta_1{}x_{1}+\ldots{}\beta_p{}x_{p}$$
GLM은 세 가지 요소로 링크 함수 g, 가중치합\(X^T\beta\)(종종 선형 예측 변수라고도 함) 및 \(E_Y\)를 정의하는 지수족(Exponential family)의 확률 분포 세가지로 구성되어 있습니다.
지수족은 지수, 분포의 평균 및 분산 및 일부 다른 매개변수를 포함하는 동일한(변수화된) 공식으로 작성할 수 있는 분포 집합입니다. 위키피디아에서는 지수족의 깔끔한 분포 목록이 소개되어 있습니다. 여기서 소개되고 있는 목록의 모든 분포는 GLM에 대해 선택할 수 있습니다. 예측하려는 결과의 유형에 따라 적절한 분포를 선택합니다. 결과가 어떤 것의 개수인가(예: 한 가정에 사는 아이들의 수)? 그렇다면 포아송 분포는 좋은 선택이 될 수 있을 것입니다. 결과는 항상 양수(예: 두 사건 사이의 시간)인가? 그렇다면 지수 분포를 선택하는 것이 가장 좋을 것입니다.
고전적인 선형 모델을 GLM의 특수한 사례로 생각해봅니다. 고전적인 선형 모델에서 가우스 분포에 대한 링크 함수는 단순히 항등함수(Identity function). 정규분포는 평균 및 분산 매개변수에 의해 매개변수로 지정됩니다. 평균은 우리가 평균적으로 기대하는 값을 설명하고 분산값은 이 평균을 중심으로 값이 얼마나 달라지는지를 설명합니다. 선형 모델에서 링크 함수는 특성값의 가중치를 정규분포의 평균에 연걸합니다.
GLM 프레임워크에서 이 개념은 모든 분포(지수족에서)와 임의 링크 함수로 일반화됩니다. 만약 y가 특정한 날에 누군가가 마시는 커피의 수와 같은 어떤 것의 개수라면, 우리는 그것을 포아송 분포와 자연 로그가 링크 함수로 사용될 수 있는 GLM으로 모델링할 수 있습니다.
$$ln(E_Y(y|x))=x^{T}\beta$$
로지스틱 회귀 모델은 베르누이 분포를 가정하고 logit 함수를 링크 함수로 사용하는 GLM이기도 합니다. 로지스틱 회귀에 사용되는 이항분포의 평균은 y가 1일 확률입니다.
$$x^{T}\beta=ln\left(\frac{E_Y(y|x)}{1-E_Y(y|x)}\right)=ln\left(\frac{P(y=1|x)}{1-P(y=1|x)}\right)$$
그리고 이 방정식을 풀어서 한 쪽에 P(y=1)가 있다면 다음과 같은 로지스틱 회귀 방정식을 얻게 됩니다.
$$P(y=1)=\frac{1}{1+exp(-x^{T}\beta)}$$
지수군으로부터의 각 분포는 분포로부터 수학적으로 도출될 수 있는 표준 연결 함수를 가지고 있습니다. GLM 프레임워크는 분포와 독립적으로 링크 함수를 선택할 수 있도록 합니다. 올바른 링크 함수를 선택하는 완벽한 방법은 없습니다. 목표값의 분포에 대한 지식뿐만 아니라 이론적 고려사항과 모델이 실제 데이터에 얼마나 잘 맞는지 고려합니다. 일부 분포의 경우 표준 링크 함수는 해당 분포에 유효하지 않은 값으로 이어질 수 있습니다. 지수 분포의 경우, 표준 링크 함수는 음의 역함수가 되어 지수 분포의 영역 밖에 있는 음수값으로 예측될 수 있습니다. 어떤 링크 함수도 선택할 수 있기 때문에, 간단한 해결책은 분포의 영역을 준수하는 다른 함수를 선택하는 것이다.
예제
GLM의 필요성을 강조하기 위해 커피 마시는 행동에 대한 데이터셋을 시뮬레이션해봅니다. 여러분이 매일매일 커피를 마시는 행동에 대한 데이터를 수집했다고 가정해봅시다. 만약 여러분이 커피를 좋아하지 않는다면, 커피 대신 차를 마신다고 가정해봅시다. 컵의 갯수와 함께 현재의 스트레스 수준을 1부터 10까지의 척도로 기록합니다. 전날 밤에 잠을 얼마나 잘 잤는지, 그리고 그날 일을 해야 했는지. 목표는 스트레스, 수면, 업무 등의 특성값을 감안하여 커피를 마신 횟수를 예측하는 것입니다. 200일 동안 데이터를 시뮬레이션을 할 때, 스트레스와 수면은 1에서 10 사이에서 균일한 확률로 나타냈고 업무는 예/아니오(Yes/No)가 50/50의 확률로 나타냈습니다. 그 다음, 각각의 날 동안 커피를 마신 횟수는 포아송 분포에서 추출하여 강도 λ(이는 또한 포아송 분포의 예상 값이기도 함)을 특성값인 수면, 스트레스 및 업무의 함수로 모델링하였다.
목표 변수의 분포, 주어진 날의 커피를 마신 횟수를 살펴보도록 합시다.
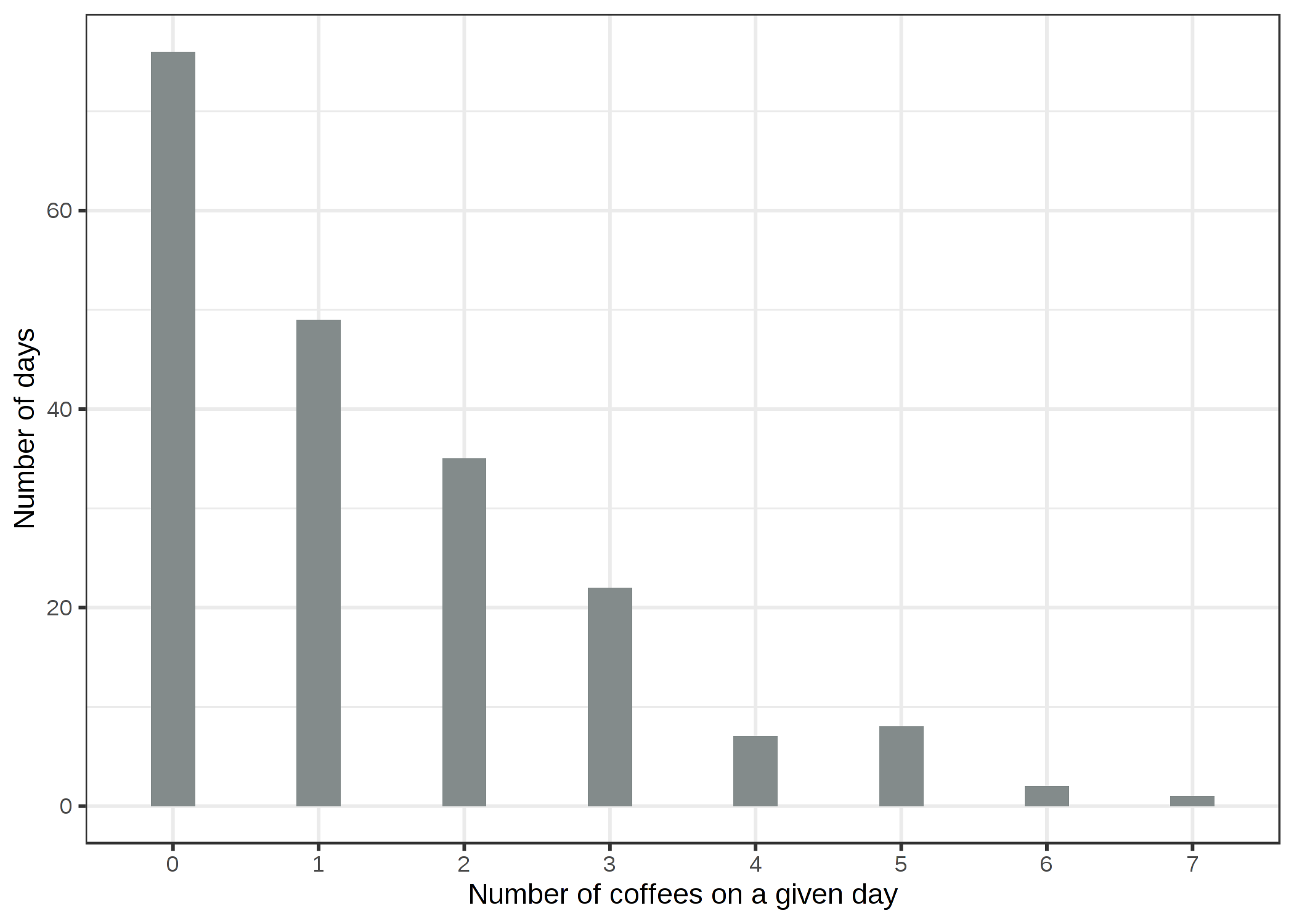
200일 중 76일은 커피를 전혀 마시지 않았고, 가장 극단적인 날에는 7번 마셨습니다. 순진하게 선형 모델을 사용하여 수면 수준, 스트레스 수준을 사용하여 커피를 마신 횟수를 예측하고 예/아니오 특성값을 수행하도록 합니다. 가우스 분포를 거짓으로 가정할 때 어떤 점이 잘못될 수 있을까요? 잘못된 가정은 추정치, 특히 가중치의 신뢰 구간을 무효화할 수 있습니다. 보다 분명한 문제는 다음 그림에서 알 수 있듯이 예측이 참된 결과의 "허용된" 영역과 일치하지 않는다는 것입니다.
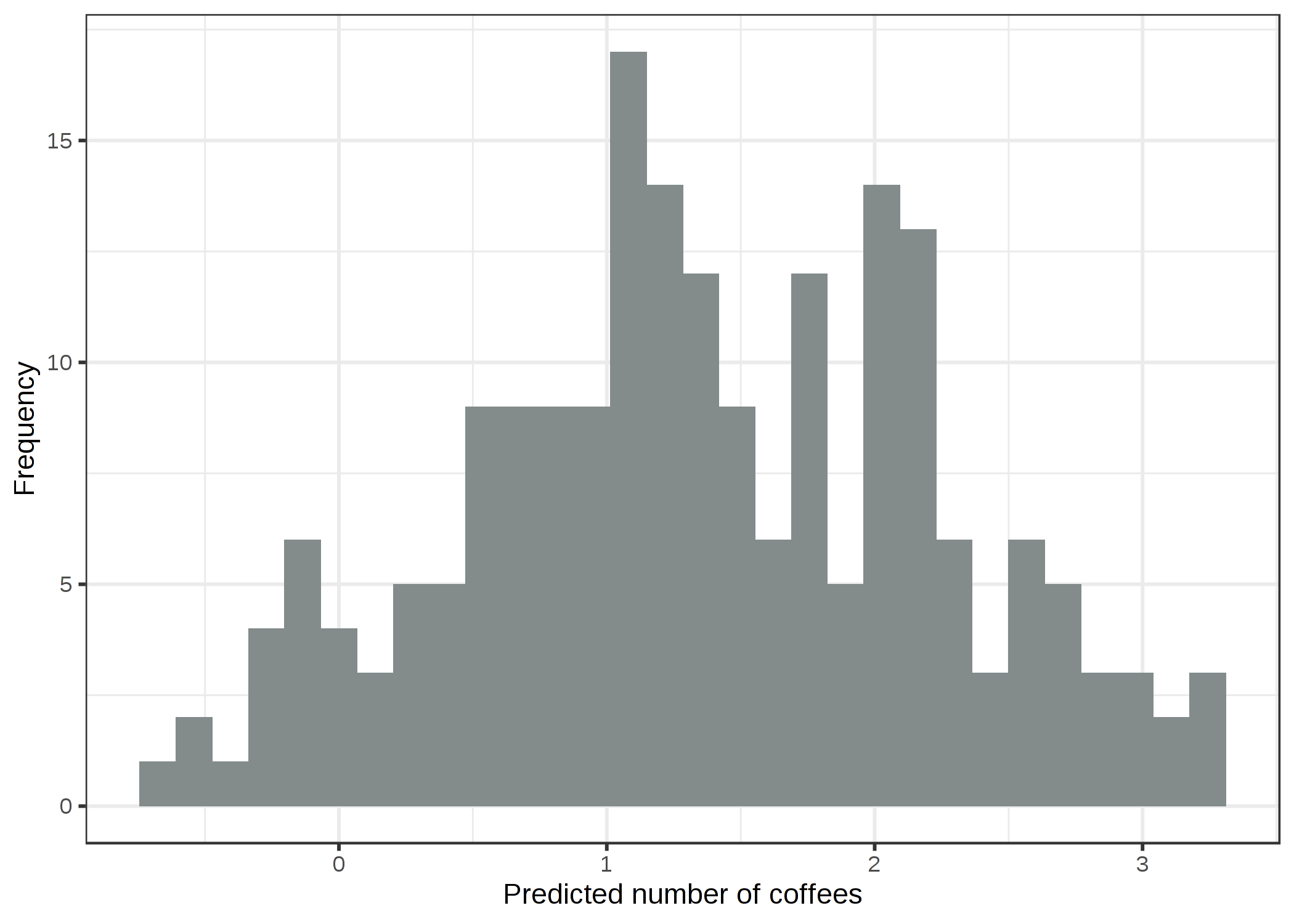
선형 모델은 음수의 횟수를 예측하기 때문에 말도 안되는 결과가 나옵니다. 이 문제는 GLM(Generalized Linear Model)으로 해결할 수 있습니다. 링크 함수와 가정된 분포를 변경할 수 있습니다. 한 가지 가능성은 가우스 분포를 유지하고 항상 항등함수 대신 log-link(역방향은 exp-function)와 같은 양수값 예측으로 이어지는 링크 함수를 사용하는 것입니다. 훨씬 더 좋은 방법은 데이터 생성 프로세스와 적절한 링크 함수에 해당하는 분포를 선택하는 것입니다. 결과가 횟수이기 때문에, 포아송 분포는 링크 함수로서의 로그와 함께 당연한 선택이 될 것입니다. 이 경우 데이터는 포아송 분포로 생성되기까지 했으므로 포아송 GLM은 완벽한 선택이 될 것입니다. 적합 포아송 GLM은 다음과 같은 예측 값 분포를 유도합니다.

이제 음의 횟수는 사라지고 훨씬 더 좋은 수치가 나타남을 확인할 수 있습니다.
GLM 가중치의 해석
링크 함수로 가정한 분포는 추정 특성값 가중치를 해석하는 방법을 결정합니다. 커피 음용 횟수 예제에서는 포아송 분포 및 로그 링크가 있는 GLM을 사용했는데, 이는 특성값과 예상 결과 사이의 다음과 같은 관계를 의미하고 있습니다.
$$ln(E(\text{coffees}|\text{stress},\text{sleep},\text{work}))=\beta_0+\beta_{\text{stress}}x_{\text{stress}}+\beta_{\text{sleep}}x_{\text{sleep}}+\beta_{\text{work}}x_{\text{work}}$$
가중치를 해석하기 위해 예상되는 결과의 로그가 아니라 예상되는 결과에 대한 특성값의 영향을 해석할 수 있도록 링크 함수를 반전해봅니다.
$$E(\text{coffees}|\text{stress},\text{sleep},\text{work})=exp(\beta_0+\beta_{\text{stress}}x_{\text{stress}}+\beta_{\text{sleep}}x_{\text{sleep}}+\beta_{\text{work}}x_{\text{work}})$$
모든 가중치값이 지수 함수에 있으므로, exp(a + b)는 exp(a) * exp(b) 이기 때문에 결과값 해석은 덧셈이 아니라 곱셈이 됩니다. 해석의 마지막 요소는 단순한 모델(Toy example)의 실제 가중치값입니다. 다음 표에는 95% 신뢰 구간과 함께 추정 가중치와 Exp(가중치)가 나열되어 있습니다.
| weight | exp(weight) [2.5%, 97.5%] | |
| (Intercept) | -0.16 | 0.85 [0.54, 1.32] |
| stress | 0.12 | 1.12 [1.07, 1.18] |
| sleep | -0.15 | 0.86 [0.82, 0.90] |
| workYES | 0.80 | 2.23 [1.72, 2.93] |
스트레스 수준을 1포인트 증가시키면 커피를 마신 횟수가 1.12배 증가합니다. 수면의 질을 1포인트 높이면 커피를 마신 횟수가 0.86배 증가합니다. 하루 커피 예상 음용 횟수는 쉬는 날보다 평균 2.23배입니다. 요약하면, 스트레스가 많을수록, 잠을 덜 자고 일을 많이 할수록, 커피를 더 많이 소비하게 됩니다.
이 섹션에서는 대상이 가우스 분포를 따르지 않을 때 유용한 일반화된 선형 모델에 대해 조금 살펴보았습니다. 다음으로, 두 특성값 사이의 상호작용을 선형 회귀 모델에 통합하는 방법을 살펴봅니다.
상호작용(Interactions)
선형 회귀 모형은 한 특성값의 효과가 다른 특성값(= 상호작용 없음)에 관계없이 동일하다고 가정합니다. 그러나 데이터에는 종종 상호작용이 존재합니다. 대여한 자전거의 수를 예측하기 위해, 온도와 근무일인지 아닌지가 상호작용이 될 수 있습니다. 아마도, 사람들이 일을 해야 할 때, 사람들은 어떤 일이 일어나더라도 자전거를 빌려서 출근하기 위해 자전거를 타게 될 것이기 때문에, 온도는 대여된 자전거의 수에 별로 영향을 미치지 않을 것입니다. 쉬는 날에는 많은 사람들이 즐거움을 위해 타지만, 날씨가 충분히 따뜻할 때만 타겟지요. 렌탈 자전거에 관하여, 온도와 근무일 사이의 상호작용을 기대할 수 있습니다.
어떻게 하면 선형 모델이 상호작용을 포함하도록 할 수 있을까요? 선형 모델을 적합시키기 전에 특성값간 상호 작용을 나타내는 특성값 행렬에 열을 추가하고 모델을 평소와 같이 적합시킨다. 선형 모델의 변경은 필요 없고 데이터의 추가 열만 필요하므로 해답은 어떤 면에서 명쾌합니다. 작업일 및 온도 예제에서는 작업하지 않는 날 동안 0이 있는 새로운 특성값을 추가하고, 그렇지 않으면 작업일을 기준 카테고리라고 가정하여 온도 특성값을 갖습니다. 데이터가 다음과 같이 주어진다고 가정해봅니다.
| Work | temp |
| Y | 25 |
| N | 12 |
| N | 30 |
| Y | 5 |
선형 모델에 의해 사용되는 데이터 표는 약간 다르게 보입니다. 다음 표는 어떤 상호작용을 지정하지 않을 경우 모델에 대해 준비된 데이터가 어떻게 나타내는지를 보여줍니다. 일반적으로 이러한 변환은 통계 소프트웨어에 의해 자동으로 수행됩니다.
| 절편 | workY | temp |
| 1 | 1 | 25 |
| 1 | 0 | 12 |
| 1 | 0 | 30 |
| 1 | 1 | 5 |
첫 번째 열은 절편값을 나타냅니다. 두 번째 열은 카테고리 특성값을 인코딩하며, 기준 카테고리는 0이고 다른 하나는 1입니다. 세 번째 열에는 온도가 포함되어있습니다.
| 절편 | workY | temp | workY.temp |
| 1 | 1 | 25 | 25 |
| 1 | 0 | 12 | 0 |
| 1 | 0 | 30 | 0 |
| 1 | 1 | 5 | 5 |
새로운 열 "workY.temp"는 특성값 근무일(work)과 온도(temp) 사이의 상호작용을 나타낸 것입니다. 이 새로운 특성값 열은 작업 특성값이 기준 카테고리(근무일이 아닌 경우 N)에 있는 경우 인스턴스에 대해 0이며, 그렇지 않으면 인스턴스 온도 특성값을 가정합니다. 이 유형의 인코딩을 사용하면 선형 모델은 두 기간 동안 온도의 다른 선형 효과를 학습할 수 있습니다. 이는 두 특성값의 상호작용 효과입니다. 상호작용 항이 없으면 카테고리 특성과 수치 특성값 결합 효과는 서로 다른 카테고리에 대해 수직으로 이동하는 선으로 설명할 수 있습니다. 상호작용을 포함하면 수치 특성값(경사)의 효과가 각 카테고리에 다른 값을 가지는 것을 허용하게 됩니다.
두 카테고리 특성값의 상호작용은 유사하게 작용됩니다. 특성값의 조합을 나타내는 추가 특성값을 만듭니다. 다음은 근무일(작업)과 카테고리 기상특성값(wthr)을 포함한 몇 가지 인위적인 데이터를 나타냅니다.
| work | wthr |
| Y | 2 |
| N | 0 |
| N | 1 |
| Y | 2 |
다음으로, 상호작용 값들을 포함합니다.
| Intercept | workY | wthr1 | wthr2 | workY.wthr1 | WorkY.wthr2 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
첫 번째 열은 절편값을 추정하는 역할을 합니다. 두 번째 열은 인코딩된 작업 특성값입니다. 3열과 4열은 기상 특성값을 위한 것으로, 3개 카테고리에 대한 효과를 포착하기 위해서는 2개의 가중치가 필요하기 때문에 2개의 열이 필요하며, 그 중 하나는 기준 카테고리입니다. 나머지 열은 상호작용을 나타냅니다. 두 특성값의 각 카테고리(기준 카테고리 제외)에 대해 두 특성값이 모두 특정 카테고리를 갖는 경우, 그렇지 않으면 0인 새로운 형상 열을 생성합니다.
두 수치적 특성값의 경우 상호작용 열을 더 쉽게 구성할 수 있습니다. 단순히 두 수치상의 특성값을 곱하면 됩니다.
상호작용 항을 자동으로 탐지하고 추가하는 방법이 있습니다. 그 중 하나는 RuleFit 을 통해 찾을 수 있습니다. RuleFit 알고리즘은 먼저 상호작용 항을 측정한 다음 상호작용을 포함한 선형 회귀 모델을 추정합니다.
예제
선형 모델 파트에서 이미 모델링한 자전거 대여 예측 작업으로 돌아가 봅시다. 이번에는 온도와 근무일 특성값 간의 상호작용을 추가로 고려합니다. 이렇게 되면 다음과 같은 추정 가중치와 신뢰 구간이 발생하게 됩니다.
| Weight | Std.Error | 2.5% | 97.5% | |
| (Intercept) | 2185.8 | 250.2 | 1694.6 | 2677.1 |
| seasonSUMMER | 893.8 | 121.8 | 654.7 | 1132.9 |
| seasonFALL | 137.1 | 161.0 | -179.0 | 453.2 |
| seasonWINTER | 426.5 | 110.3 | 209.9 | 643.2 |
| holidayHOLIDAY | -674.4 | 202.5 | -1071.9 | -276.9 |
| workingdayWORKING DAY | 451.9 | 141.7 | 173.7 | 730.1 |
| weathersitMISTY | -382.1 | 87.2 | -553.3 | -211.0 |
| weathersitRAIN/… | -1898.2 | 222.7 | -2335.4 | -1461.0 |
| temp | 125.4 | 8.9 | 108.0 | 142.9 |
| hum | -17.5 | 3.2 | -23.7 | -11.3 |
| windspeed | -42.1 | 6.9 | -55.5 | -28.6 |
| days_since_2011 | 4.9 | 0.2 | 4.6 | 5.3 |
| workingdayWORKING DAY:temp | -21.8 | 8.1 | -37.7 | -5.9 |
추가 상호작용 효과는 음수(-21.8)이며, 0을 포함하지 않는 95% 신뢰 구간에서 알 수 있듯이 0과 크게 다릅니다. 반면에, 그 데이터는 iid(독립 항등 분포, independent and identically distributed) 가 아닙니다. 왜냐하면 서로 가까운 날들은 서로 독립적이지 않기 때문입니다. 신뢰 구간은 오해의 소지가 있을 수 있으니, 액면 그대로 받아들이지 않으셔도 됩니다. 상호작용 용어는 관련 특성값의 가중치 해석을 변경합니다. 업무일로 볼 때 온도가 부정적인 영향을 미치는가? 그 답은 비록 테이블이 학습되지 않은 사용자에게 이를 제안한다 하더라도 답이 아닙니다. "업무일"을 해석할 수 없습니다. “workingdayWORKING DAY:temp” 상호작용 가중치는 "다른 모든 특성값은 변경하지 않고 근무일에 온도의 상호작용 효과를 증가시키면 예상 자전거 대여수가 감소한다"는 해석이 가능하기 때문에 분리되어 있습니다. 그러나 상호작용 효과는 온도의 주효과만을 더해줄 뿐입니다. 그날을 근무일이라고 가정하고 만약 오늘 기온이 1도 더 따뜻하다면 무슨 일이 일어날지 알고 싶어집니다. 그러면 우리는 "temp"과 "workingdayWORKING DAY:temp"의 가중치를 모두 합산해야 합니다. 예상치가 얼마나 증가하는지 확인해봅니다.
상호작용을 시각적으로 이해하는 것이 더 쉽습니다. 카테고리와 수치 특성값 사이의 상호관계를 적용함으로서, 하나의 온도 대신 두 개의 경사값을 얻을 수 있습니다. 일을 하지 않아도 되는 날('NO WORKING DAY')의 온도 기울기는 표를 통해 직접 확인할 수 있습니다(125.4). 일을 하는 날('WORKING DAY')의 온도 기울기는 두 온도 가중치의 합니다.(125.4-21.8-103.6) 온도=0에서 'NO WORKING DAY'의 절편값은 선형 모델의 절편에 의해 결정됩니다(2185.8). 온도=0에서 'WORKING DAY'의 절편값은 절편값+근무일의 효과 로 결정되어집니다(2185.8+451.9=2637.7).

비선형효과 - GAMs
세상은 항상 선형만 존재하지 않습니다. 선형 모델의 선형성은 특정 특성값에 어떤 가치가 있든 간에 한 단위씩 값을 증가시키는 것은 항상 예측된 결과에 동일한 영향을 미친다는 것을 의미합니다. 섭씨 10도에서 온도를 1도씩 올리면 40도가 되었을 때 온도가 1도씩 상승하는 것과 같은 효과가 렌털 자전거의 수에도 영향이 있다고 보는 것이 타당할까요? 직관적으로 10도에서 11도로 온도를 높이면 자전거 대여량에 긍정적인 영향을 미치고 40도에서 41도로는 부정적인 영향을 줄 것으로 예상할 수 있는데, 이 역시 책에 나와 있는 많은 예에서 볼 수 있습니다. 온도 특성값은 대여 자전거의 수에 선형적이고 긍정적인 영향을 미치지만, 어느 순간에는 평평해지고 심지어 고온에서 부정적인 영향까지 미치게 됩니다. 선형 모델은 신경쓰지 않으며, (유클리드 거리를 최소화함으로써) 가장 좋은 선형 평면을 찾을 것입니다.
다음 기술 중 하나를 사용하여 비선형 관계를 모델링할 수 있습니다.
- 특성값의 단순한 변형(logarithm)
- 특성값의 카테고리화
- Generalized Additive Models (GAMs)
각각의 방법에 대해 자세히 설명하기 전에, 먼저 세 가지 방법을 모두 설명하는 예를 들어 보겠습니다. 자전거 대여 데이터셋을 가지고 온도 특성값만 갖춘 선형 모델을 훈련시켜 대여 자전거의 수를 예측해봅니다. 다음 그림은 표준 선형 모델, 변환된 온도의 선형 모델(logarithm)을 사용하여 추정된 기울기를 나타내며, 이는 온도가 카테고리 특성값으로 처리되고 회귀 스플라인(GAM)을 사용하는 선형 모델입니다.
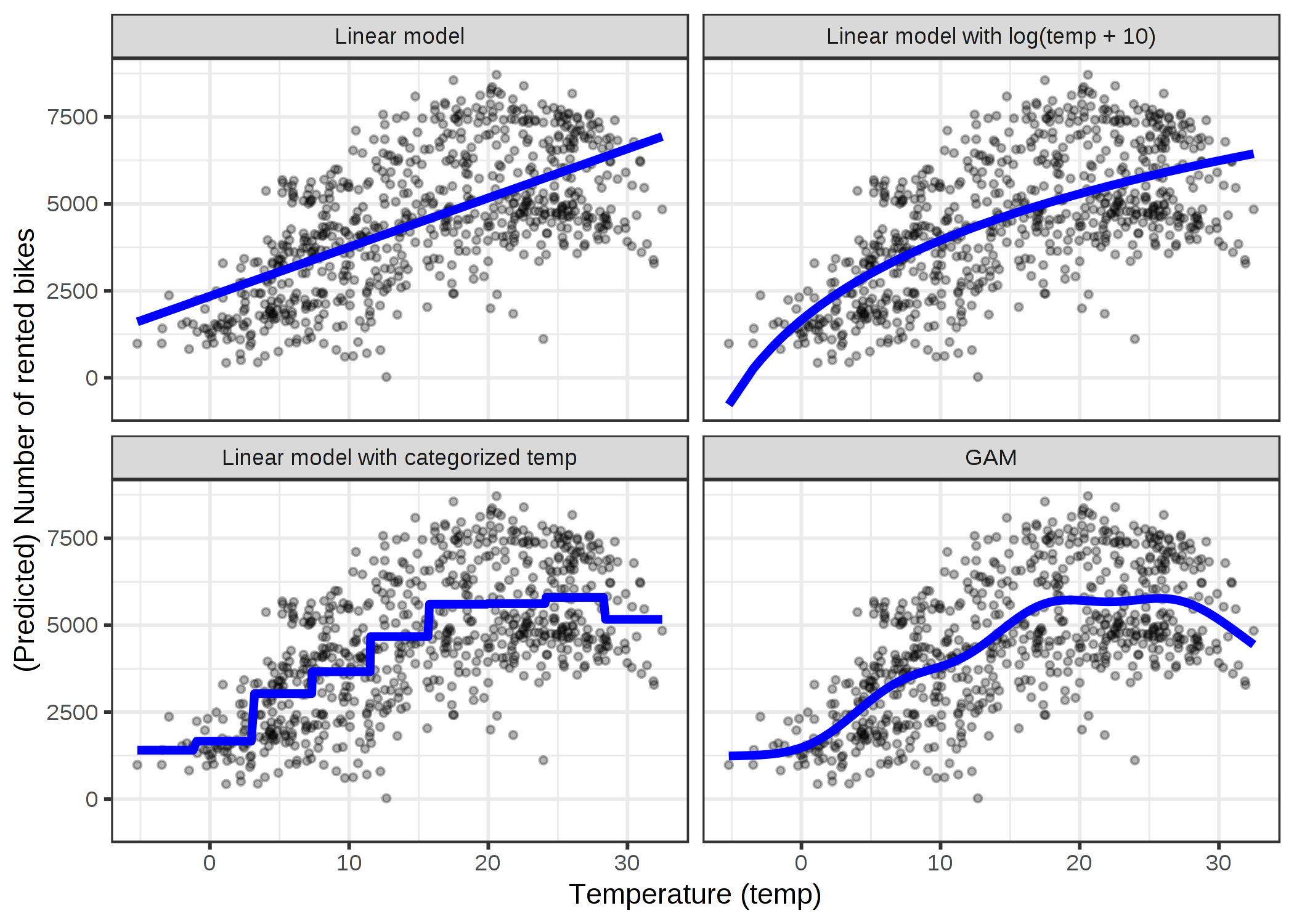
특성값 변환
종종 특성값의 로그는 변환으로 사용된다. 로그(Logarithm)를 사용하면 온도가 10배 상승할 때마다 자전거의 대여숫자에 동일한 선형 효과가 있으므로 섭씨 1도에서 섭씨 10도로 변경하면 0.1에서 1로 변경되는 것과 같은 효과가 있다(뭔가 잘 납득이 되지는 않습니다). 특성값 변환의 다른 예로는 제곱근, 제곱함수 및 지수함수가 있습니다. 특성값 변환을 사용하면 데이터에서 이 특성값의 열을 Logarithm과 같은 특성값의 함수로 교체하고, 평상시와 같이 선형 모형을 적합시킬 수 있습니다. 일부 통계 프로그램에서는 선형 모델의 호출에 변환을 지정할 수도 있습니다. 특성값을 변환할 때 창조적일 수 있습니다. 특성값의 해석은 선택한 변환에 따라 변합니다. 로그 변환을 사용할 경우 선형 모델의 해석은 "형상의 로그가 1씩 증가하면 해당 중량에 의해 예측이 증가한다"가 됩니다. 항등함수가 아닌 링크 기능이 있는 GLM을 사용하면 해석이 더욱 복잡해지는데, 그 이유는 두 변환을 해석에 통합해야 하기 때문입니다(로그나 exp와 같이 서로 항등하무가 되는 경우를 제외합니다, 그러면 해석이 쉬워집니다).
특성값 카테고리화
비선형 효과를 얻을 수 있는 또 다른 가능성은 특성값을 불연속으로 이산하는 것입니다. 특성값을 카테고리형 특성값으로 바꾸는 것입니다. 예를 들어, 온도 특성값을 [-10, -5), [-5, 0, ... 등과 함께 20개의 간격으로 줄일 수 있습니다. 연속 온도 대신 분류된 온도를 사용하면 선형 모델은 각 레벨이 자체 추정치를 얻기 때문에 단계 함수를 추정할 수 있습니다. 이 접근방식의 문제점은 더 많은 데이터가 필요하고, 적합도가 더 높고, 특성값을 의미 있게 구별하는 방법이 불분명하다는 것입니다(같은 간격 또는 정량적인가? 얼마나 간격이 떨어져있는가?). 어떤 데이터가 아주 강력한 경우의수가 있을 경우에만 카테고리화 방법을 사용할 것입니다. 예를 들어, 다른 연구와 비교 가능한 모델을 만드는 것이다.
Generalized Additive Models (GAMs)
왜 (일반화된) 선형 모델이 비선형 관계를 학습하도록 '단순하게' 않는걸까요? 그것이 GAMs을 사용하는 이유입니다. GAMs는 관계가 단순한 가중치 합이어야 한다는 제한을 완화시키고 대신에 각 특징의 임의 함수의 합에 의해 결과를 모델링할 수 있다고 가정합니다. 수학적으로 GAM의 관계는 다음과 같이 나타냅니다.
$$g(E_Y(y|x))=\beta_0+f_1(x_{1})+f_2(x_{2})+\ldots+f_p(x_{p})$$
이 공식은 선형 항 \(\beta_j{}x_{j}\) 보다 유연한 함수 \(f_j(x_{j})\)로 대체된다는 차이를 갖는 GLM 공식과 유사하다. GAM의 핵심은 여전히 특성값 효과의 합이지만, 일부 특성값과 출력 사이의 비선형 관계를 허용하는 옵션이 있습니다. 선형효과도 프레임워크에 의해 커버되는데, 특성값을 선형적으로 처리하기 위해서는 \(f_j(x_{j})\)를 \(x_{j}\beta_j\)의 양식으로만 제한할 수 있기 때문입니다.
가장 큰 문제는 비선형 함수를 어떻게 학습시키냐는 것입니다. 그 답은 "스플라인" 또는 "스플라인 함수"에서 찾을 수 있습니다. 스플라인(Splines)은 임의의 함수를 근사하게 하기 위해 조합할 수 있는 함수입니다. 좀 더 복잡한 것을 만들기 위해 레고 벽돌을 쌓는 것과 같습니다. 이러한 스플라인 함수를 정의하는 방법은 헷갈릴 수 있습니다. 만약 여러분이 스플라인을 정의하는 모든 방법에 대해 더 많이 배우고 싶다면, 상당한 노력이 필요할 것입니다. 여기서는 자세히 설명하지 않고 직관적으로 접근하고자 합니다. 개인적으로 스플라인을 이해하는 데 가장 도움이 된 것은 개별 스플라인 기능을 시각화하고 데이터 표가 어떻게 수정되는지 알아보는 것이었습니다. 예를 들어 스플라인으로 온도를 모델링하기 위해 데이터에서 온도 특성값을 제거하고 각각 스플라인 함수를 나타내는 4열로 교체합니다. 보통은 더 많은 스플라인 함수를 가지고 있을 것입니다. 여기서는 단지 예시를 위해 숫자를 줄였을 뿐입니다. 이러한 새로운 스플라인 특성값의 각 인스턴스(instance)의 값은 인스턴스(instance)의 온도 값에 따라 달라집다. 모든 선형 효과와 함께, GAM은 또한 이러한 스플라인 가중치를 추정합니다. GAMs는 또한 가중치가 0에 가깝게 유지되도록 하기 위해 가중치에 패널티를 도입합니다. 이는 스플라인 유연성을 효과적으로 감소시키고 오버핏을 감소시킨다. 곡선의 유연성을 제어하는 데 일반적으로 사용되는 매끄러운 매개변수는 교차 검증을 통해 조정됩니다. 페널티 용어를 무시한 채 스플라인을 이용한 비선형 모델링은 화려한 특성값 엔지니어링입니다.
온도만 사용하여 GAM을 사용하는 자전거 대여수를 예측하는 예에서 모델 특성표는 다음과 같습니다.
| (Intercept) | s(temp).1 | s(temp).2 | s(temp).3 | s(temp).4 |
| 1 | 0.93 | -0.14 | 0.21 | -0.83 |
| 1 | 0.83 | -0.27 | 0.27 | -0.72 |
| 1 | 1.32 | 0.71 | -0.39 | -1.63 |
| 1 | 1.32 | 0.70 | -0.38 | -1.61 |
| 1 | 1.29 | 0.58 | -0.26 | -1.47 |
| 1 | 1.32 | 0.68 | -0.36 | -1.59 |
각 행은 데이터의 개별 인스턴스를 나타냅니다(1일). 각 스플라인 열에는 특정 온도 값에서 스플라인 함수의 값이 포함되어 있습니다. 아래 그림은 이러한 스플라인 함수의 모양을 보여줍니다.

GAM은 각 온도 스플라인 특성값에 가중치를 부여합니다.
| weight | |
| (Intercept) | 4504.35 |
| s(temp).1 | -989.34 |
| s(temp).2 | 740.08 |
| s(temp).3 | 2309.84 |
| s(temp).4 | 558.27 |
그리고 추정된 가중치로 가중된 스플라인 함수의 합계에서 발생하는 실제 곡선은 다음과 같이 나타냅니다.

매끄러운 효과를 해석하려면 적합곡선을 육안으로 점검해야 합니다. 스플라인은 보통 평균 예측을 중심으로 이루어지기 때문에 곡선의 점은 평균 예측과의 차이점이다. 예를 들어 섭씨 0도에서 예상 자전거 수는 평균 예측치보다 3000개 낮습니다.
장점
지금까지 다루었던 내용들은 선형 모델을 확장하는 방법들 중 극히 일부분입니다. 선형 모델에서 어떤 문제에 직면하든, 여러분들은 아마도 이를 해결하는 확장방법을 발견할 것입니다.
대부분의 방법들은 수십년 동안 사용되어 왔습니다. 예를 들어, GAM은 2019년을 기준으로 거의 30년동안 사용되었습니다. 산업계의 많은 연구원들과 실무자들은 선형 모델에 대해 많은 경험을 가지고 있으며, 그러한 방법들은 모델링을 위한 현상으로서 수많은 학계나 업게에서 사용되고 있습니다.
예측하는 것 외에도 모델을 사용하여 추론하고, 모델의 가정이 어긋나지 않는 한 데이터에 대한 결과를 도출할 수 있습니다. 가중치, 유의성 겁사, 예측 구간 등에 대한 신뢰 구간을 얻을 수 있습니다.
통계 소프트웨어는 보통 GLM, GAM 뿐만 아니라 더욱 특별한 선형 모델에 적합하도록 매우 좋은 인터페이스를 가지고 있습니다.
수많은 기계학습 모델의 불투명성은 1)자료 희박성의 부족(Lack of sparseness), 즉 많은 특성값이 사용되고 있는지, 2) 비선형 방식으로 처리되는 특성값이 나타나며, 그 효과를 설명하기 위해 단일 가중치 이상이 필요하며, 3) 특성값의 상호작용을 모델링하는 데에서 비롯됩니다. 선형 모델이 해석력이 높지만 적합성이 낮은 경우가 많다고 가정할 때, 여기서 설명한 확장은 해석력을 일부 보존하면서 보다 유연한 모델로 원활하게 전환할 수 있는 좋은 방법을 제공합니다.
단점
단순한 선형 모델을 확장할 수 있는 방법은 엄청나게 많습니다. 많은 연구자들과 실무자들의 커뮤니티는 같은 기능을 수행하는 모델임에도 연구자들 혹은 실무자들이 해당 모델에 다른 이름을 붙여 매우 혼란스러운 경우가 있습니다.
선형 모델을 대부분 수정하면 모델을 해석하는 것이 더욱 어려워집니다. 항등함수가 아닌 링크함수(GLM)는 해석을 복잡하게 하고, 상호작용도 해석을 복잡하게 하여, 비선형 특성 효과는 직관적이지 못하거나 (로그 변환과 같이) 더이상 단일한 숫자(스플라인 함수)로 요약할 수 없습니다.
GLM, GAM은 데이터 생성 프로세스에 대한 가정에 의존합니다. 만약 규칙이 어긋나게 되면, 가중치의 해석은 더이상 유효하지 않게 됩니다.
랜덤 포레스트나 Gradient tree boosting과 같은 트리 기반 앙상블의 성능은 대부분의 경우 가장 정교한 선형 모델보다 더 좋습니다. 이는 부분적으로 kaggle.com과 같은 플랫폼에서 우수한 모델들로부터 볼 수 있습니다.
소프트웨어
여기서 소개된 모든 예쩨는 R 언어를 사용하여 만들어졌습니다. GAM의 경우, gam package가 사용되었으나 그밖에 많은 것들이 사용되었습니다. R은 선형 회귀 모델을 확장하기 위한 엄청난 양의 패키지를 가지고 있습니다. 다른 분석 언어와는 타의 추종을 불허하는 R은 선형 회귀 모델 확장의 모든 가능한 확장 프로그램입니다. Python에서 GAM(pyGAM)의 구현을 찾을 수 있지만, R에 비해서는 약간 빈약한 면이 있습니다.
추가 확장
선형 모델에서 직면할 수 있는 문제들에 대한 내용을 다루어보았습니다. 좀 더 자세한 내용을 알고 싶으신 분들은 검색 엔진을 통해 더 많은 자료들을 찾아보시길 바랍니다.
제 데이터는 독립적이고 동일한 분포(iid)라는 가정이 위배되고 있습니다.
예를 들어, 같은 환자에 대하여 반복적인 측정을 수행합니다.
→혼합 모델(Mixed model) 혹은 일반화 추정 방정식(Generalized extimation equation)
제 모델에는 이질적인 오류가 발생합니다.
예를 들어, 주택의 가격을 예측할 때, 모델 오류는 보통 비싼 주텍에서 더 높기 때문에 선형 모델의 균일성이 위배됩니다.
→Robust 회귀 분석(Robust regression)
제 모델에 강한 영향을 미치는 이상점(outlier)이 있습니다.
→Robust 회귀 분석(Robust regression)
저는 어느 한 사건이 일어날 때까지의 시간을 예측하고자 합니다.
사건 발생 시간 데이터는 일반적으로 검열된 측정과 함께 제공되는데, 이는 일부의 경우 사건을 관찰할 시간이 부족하다는 것을 의미합니다. 예를 들어, 한 회사는 얼음 기계의 고장을 예측하고 싶어 하지만, 2년 동안의 데이터를 가지고 있습니다. 일부 기계는 2년이 지나도 여전히 제대로 동작하고 있지만 나중에는 고장이 날 가능성이 있습니다.
→모수적 생존모형(Parametric survival model), cox 회귀(Cox regression), 생존 분석(survival analysis)
제 모델의 예측 결과는 카테고리입니다.
만약 결과에 두 개의 카테고리가 있는 경우, 카테고리에 대한 확률을 모델링하는 로지스틱 회귀 모델을 사용합니다.
→더 많은 카테고리가 있다면 다항식 회귀(Multinomial regression)에 대해 검색하십시오. 로지스틱 회귀 분석과 다항식 회귀 분석 모두 GLM입니다.
저는 순서 있는 카테고리에 대해 예측하고자 합니다.
예를 들면 학점순과 같은 경우입니다.
→비례 오즈 모델(Propotional odds model)
제 데이터의 결과는 횟수(한 가족의 아이들의 수)입니다.
→포아송 회귀(Poisson regression)
포아송 모델은 GLM이기도 합니다. 0의 갯수가 매우 빈번한 문제도 있을 수 있습니다.
→영과잉 포아송 회귀(Zero-inflated Poisson regression), 허들 모델(Hurdle model)
저는 정확한 인과관계 결과를 도출하기 위해 어떤 특성값을 모델에 포함시켜야 하는지 확신할 수가 없습니다.
예를 들어, 약물이 협압에 미치는 영향을 알고 싶은데, 이 약이 어떤 혈액 수치에 직접적인 영향을 미치고 그 혈행의 수치는 결과에 영향을 미칩니다. 혈액 수치를 회귀 모델에 포함해야 하나요?
→인과 추론(Causal inference), Mediation 분석(Mediation analysis)
데이터가 누락되었습니다.
→다중 대치법(Multiple imputation)
제 모델의 사전 지식(Prior knowledge)을 통합하고자 합니다.
→베이즈 추론(Bayesian inference)
요즘 기분이 우울합니다.
→Amazon Alexa Gone Wild!!!
참고자료: https://christophm.github.io/interpretable-ml-book/extend-lm.html
4.3 GLM, GAM and more | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 4. 해석할 수 있는 모델' 카테고리의 다른 글
| [해석할 수 있는 기계학습(4-6)] 룰핏(RuleFit) (0) | 2020.03.01 |
|---|---|
| [해석할 수 있는 기계학습(4-5)] 의사결정 규칙(Decision Rule) (0) | 2020.02.24 |
| [해석할 수 있는 기계학습(4-4)] 의사결정 트리(Decision Tree) (1) | 2020.01.04 |
| [해석할 수 있는 기계학습(4-2)] 로지스틱 회귀 (0) | 2019.12.24 |
| [해석할 수 있는 기계학습(4-1)] 선형 회귀 (0) | 2019.12.06 |




