늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(4-4)] 의사결정 트리(Decision Tree) 본문
[해석할 수 있는 기계학습(4-4)] 의사결정 트리(Decision Tree)
Justin T. 2020. 1. 4. 01:59
특성값 및 결과값 간의 관계가 비선형적이거나 서로 상호작용하는 상황에서는 선형 회귀 및 로지스틱 회귀 모델을 사용하는 것이 적합하지 않습니다. 이러한 데이터에는 의사결정 트리(Decision Tree)이 빛을 발하게 됩니다! 트리 기반 모델은 특성값의 특정 컷오프 값에 따라 데이터를 여러 분 분할합니다. 분할을 통해 각 인스턴스가 하나의 부분 집합에 속하는 데이터 집합의 서로 다른 부분 집합이 생성됩니다. 최종 부분집합을 말단(Terminal) 또는 리프 노드(Leaf node)라고 하고 중간 부분집합을 내부 노드 혹은 분할 노드라고 합니다. 각 리프 노드의 결과를 예측하기 위해 이 노드의 학습 데이터의 평균 결과를 사용합니다. 트리는 분류와 회귀에 사용할 수 있습니다.
트리를 기를 수 있는 다양한 알고리즘들이 있습니다. 이 알고리즘들은 트리의 가능한 구조(노드 당 분할 수), 분할을 찾는 방법, 분할을 중지하는 시기 및 리프 노드 내의 단순 모델을 추정하는 방법에서 서로 다릅니다. 분류 및 회귀 트리(Classification And Regression Tree)알고리즘은 아마도 트리 유도에 가장 인기 있는 알고리즘일 것입니다. 여기서는 CART에 초점을 맞출 것이지만 그 해석은 대부분의 다른 트리 타입에서 비슷합니다. CART에 대한 자세히 알고 싶으신 분들은 다음 링크를 통해 알아보실 수 있습니다.
아래의 공식은 결과값 y와 특성값 x의 관계를 설명합니다.
$$\hat{y}=\hat{f}(x)=\sum_{m=1}^Mc_m{}I\{x\in{}R_m\}$$
각 인스턴스는 정확히 하나의 리프 노드에 도달합니다(=부분집합 \(R_m\)). \(I_{\{x\in{}R_m\}}\)는 항등함수로서 만약 x가 \(R_m\)의 부분집합일 경우 1을, 그렇지 않은 경우 0을 return 합니다. 만약 어떤 인스턴스가 리프노드 \(R_l\)에 도달하면 \(c_l\)이 리프 노드 \(R_l\) 내의 모든 학습된 인스턴스의 평균이라 하였을 때, 예측결과값은 \(\hat{y}=c_l\)입니다.
하지만 부분집합은 어디에서 비롯되는 것일까요? 이는 매우 간단합니다. CART는 특성값을 취하여 회귀 작업에 대한 y의 분산 또는 분류 작업에 대한 y의 클래스 분포에 대한 지니 지수를 최소화하는 컷오프 지점을 결정합니다. 이 분산은 노드의 y값이 평균값 주위에 얼마나 분산되어 있는지를 보여줍니다. 지니 지수는 노드가 얼마나 "불순"한지 알려줍니다. 예를 들어, 모든 클래스의 빈도가 같을 경우 노드는 불순하고, 한 클래스만 있으면 최대로 순수하다고 볼 수 있습니다. 분산 및 지니 지수는 노드의 데이터 포인트가 y에 대해 매우 유사한 값을 가질 때 최소화됩니다. 결과적으로, 최상의 컷오프 지점은 목표 결과값과 관련하여 두 결과 부분집합을 최대한 다르게 만듭니다. 카테고리 특성값의 경우 알고리즘은 다른 카테고리의 그룹화를 시도하여 부분집합을 생성하려고 합니다. 특성값당 최선의 컷오프가 결정되면 알고리즘은 분산 또는 지니 지수 측면에서 최상의 파티션을 얻을 수 있는 분할 특성값을 선택하고 이 분할을 트리에 추가합니다. 알고리즘은 정지 기준에 도달할 때까지 두 개의 새로운 노드에서 이 검색 및 분할을 반복적으로 계속 진행합니다. 가능한 기준은 분할 전 노드에 있어야 하는 최소 인스턴스 수 또는 말단 노드에 있어야 하는 최소 인스턴스 수입니다.
해석
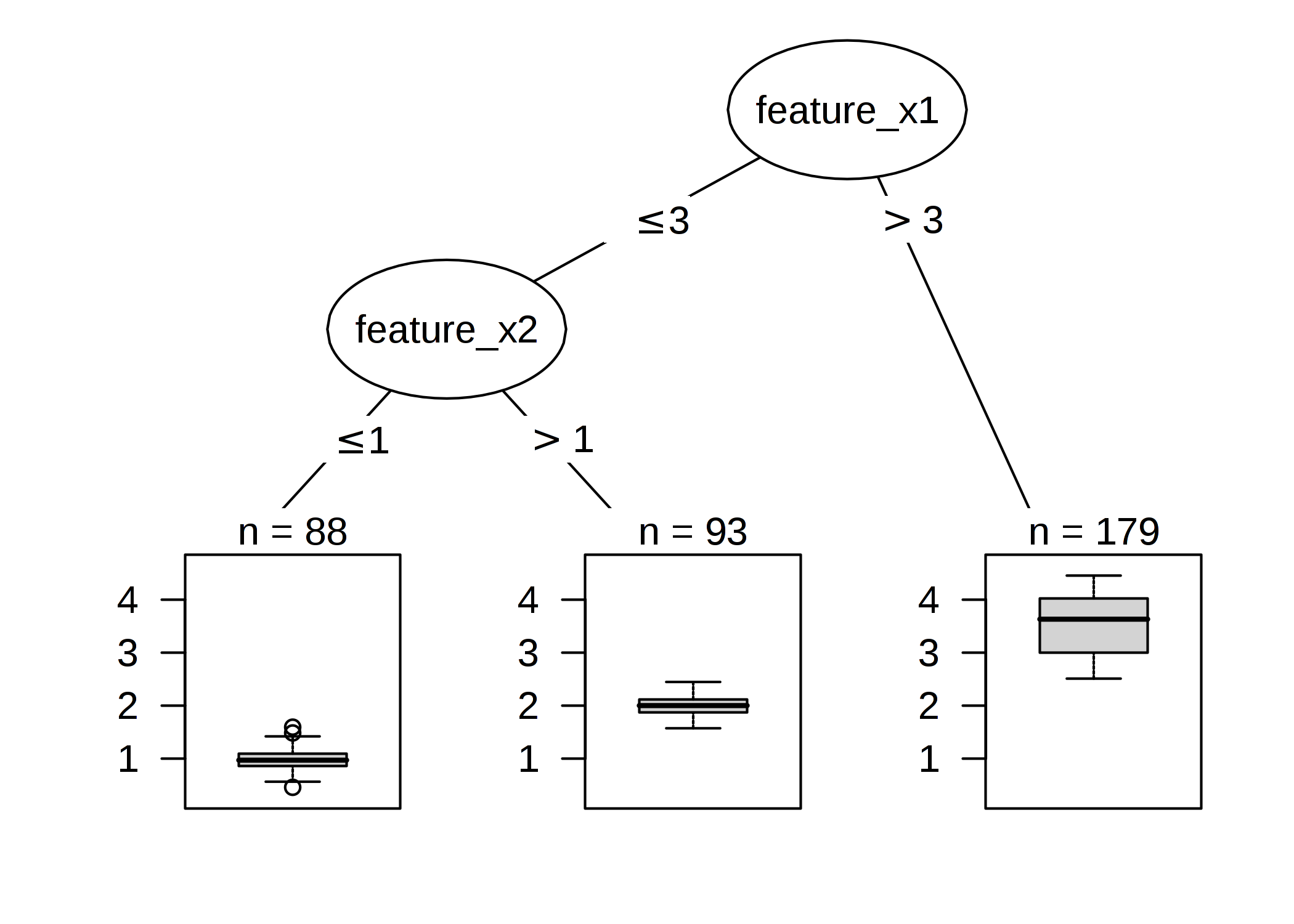
해석은 간단합니다. 루트 노드에서 시작하여 다음 노드로 이동하고 edge는 보고 있는 부분집합을 알려줍니다. 일단 리프 노드에 도달하면 그 노드는 예측된 결과를 알려줍니다. 모든 edge는 'AND'로 연결됩니다.
템플릿: 특성값 x가 임계값 c AND보다 [작거나/크거나] ... 인 경우, 예측 결과는 해당 노드의 인스턴스 y의 평균값입니다.
특성값의 중요도
의사결정 트리에서 특성값의 전반적인 중요도는 다음과 같은 방법으로 계산할 수 있습니다. 특성값이 사용된 모든 분할을 검토하고 모 노드에 비해 분산 또는 지니 지수를 얼마나 감소시켰는지를 측정합니다. 모든 중요도의 합계는 100으로 조정됩니다. 이는 각각의 중요도가 전체 모델의 중요도의 몫으로 해석될 수 있다는 것을 의미합니다.
트리 분할
의사결정 트리의 개별 예측은 의사결정 경로를 특성값당 하나의 구성요소로 분해하여 설명할 수 있습니다. 트리를 통해 결정을 추적하고 각 의사결정 노드에서 추가된 기여에 의한 예측을 설명할 수 있습니다.
의사결정 트리의 루트 노드가 출발점입니다. 만약 루트 노드를 사용하여 예측한다면, 이는 훈련된 데이터의 결과의 평균을 예측할 것입니다. 다음 분할을 사용하면 경로의 다음 노드에 따라 이 합계에 항을 빼거나 추가합니다. 최종 예측값에 이르기 위해서는 설명하고자 하는 데이터 인스턴스의 경로를 따라 계속 공식을 추가해야 합니다.
$$\hat{f}(x)=\bar{y}+\sum_{d=1}^D\text{split.contrib(d,x)}=\bar{y}+\sum_{j=1}^p\text{feat.contrib(j,x)}$$
개별 인스턴스의 예측은 목표 결과값의 평균에 루트 노드와 인스턴스가 끝나는 말단 노드 사이에 발생하는 D 분할의 모든 기여의 합을 더한 것입니다. 그러나 분할 기여에 관심이 없고 특성값 기여에 집중해야 합니다. 특성값은 둘 이상의 분할에 사용될 수도 있고 전혀 사용되지 않을 수도 있습니다. 각 p 특성값에 대한 기여도를 추가하고 각 특성값이 예측에 얼마나 기여했는지에 대한 해석을 얻을 수 있습니다.
예제
이전에 다루었던 자전거 대여 데이터를 다시 한 번 다루어보겠습니다. 의사결정 트리에 있는 특정 날에 대여된 자전거의 수를 예측하고자 합니다. 학습된 트리는 다음과 같습니다.
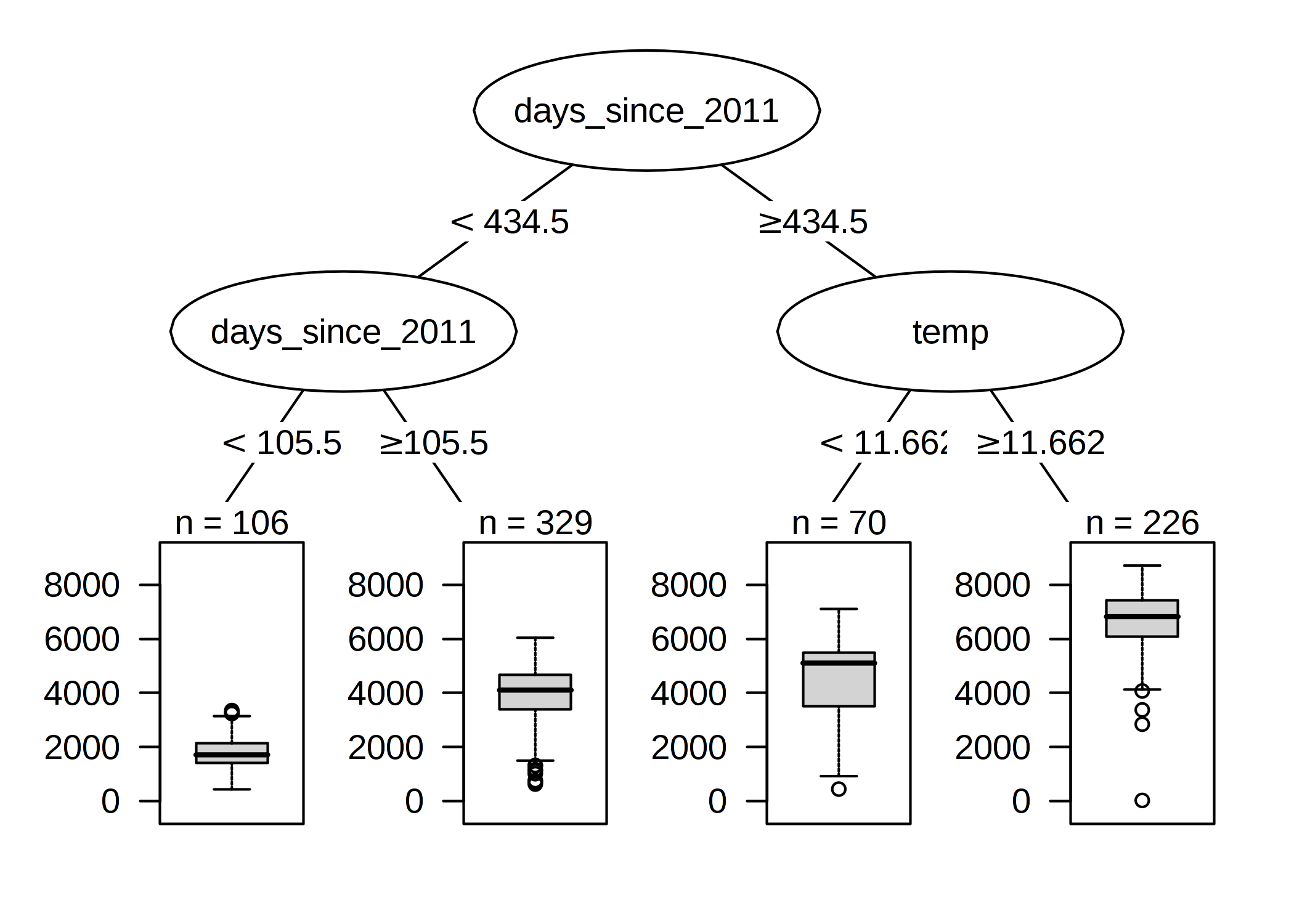
첫 번째 분할과 두 번째 분할들의 days_since_2011과 temp 중 하나는 추세 특성값으로 수행되었는데, 이는 데이터 수집이 시작된 이후의 일수를 계산하고 시간이 지나면서 자전거 대여 서비스가 더 인기를 끌고 있다는 추세를 반영합니다. 105일 전 며칠 동안 예상 자전거 대여수는 1800여 대, 106일에서 430일 사이는 3900여 대입니다. 430일 이후 며칠동안 예측은 4600(온도가 12도 이하일 경우) 또는 6600(온도가 12도 이상일 경우)입니다.
특성값의 중요도는 한 특성값이 모든 노드의 순도를 개선하는 데 얼마나 도움이 되었는지를 말해줍니다. 여기서 자전거 대여 수를 예측하는 것이 회귀 작업이기 때문에 분산이 사용되었습니다.
시각화된 트리는 온도 및 시간 추세가 분할에 사용되었음을 보여주지만 어떤 특성값이 더 중요한지를 정량화하지는 않습니다. 특성값의 중요도 측정은 시간 추세가 온도보다 훨씬 더 중요하다는 것을 보여줍니다.

장점
트리 구조는 데이터의 특성값 간의 상호작용을 포착하는 데 이상적입니다.
데이터는 선형 회귀와 같이 다차원 초평면상의 점보다 이해하기 쉬운 뚜렷한 그룹으로 귀결됩니다. 해석은 논쟁의 여지 없이 꽤 간단합니다.
트리 구조는 또한 그 노드와 edge를 가진 자연적인 시각화를 가지고 있습니다.
트리는 "인간 친화적 설명"에 대한 포스팅에서 정의한 대로 좋은 설명을 만들어줍니다. 트리 구조는 자동으로 개별 인스턴스에 대해 예측된 값을 반사실적으로 생각하도록 요청합니다. 다음과 같은 시나리오를 생각해봅니다.
"특성값이 분할점보다 크거나 작은 경우 예측값은 y2 대신 y1이 되었을 것입니다. 인스턴스의 예측과 관련성을 항상 비교할 수 있기 때문에 트리 설명은 대조적입니다."
위와 같은 시나리오(트리에 의해 정의됨)는 단순히 트리의 다른 리프노드입니다. 나무가 하나에서 세 개의 깊게 갈라지는 것처럼 짧다면, 결과적읜 설명은 선택적입니다. 깊이가 3인 트리는 개별 인스턴스의 예측에 대한 설명을 생성하기 위해 최대 3개의 특성값과 분할점을 필요로 합니다. 예측의 진실성은 트리의 예측 성능에 달려있다. 짧은 트리에 대한 설명은 매우 간단하고 일반적입니다. 왜냐하면 각각의 분할에 대한 인스턴스는 한 리프 또는 다른 리프로 떨어지고, 이전 결정은 이해하기 쉽기 때문입니다.
특성값을 변환할 필요는 없습니다. 선형 모델에서는 특성값의 로그가 필요할 때가 있습니다. 의사결정 트리는 특성값의 단조로운 변환과 동일하게 잘 작용합니다.
단점
트리는 선형 관계를 다루지 못합니다. 입력 특성값과 결과 사이의 선형 관계는 분할에 의해 근사치되어 단계 함수를 생성해야 합니다. 이는 결코 효율적이지 않습니다.
이러한 이유는 매끄러움의 부족과 관련이 있습니다. 입력 특성값의 약간의 변화는 예측 결과에 큰 영향을 미칠 수 있는데, 이는 대개 바람직하지 않습니다. 집의 가치를 예측하는 트리와 그 트리가 집의 크기를 분할 특성값의 하나로 사용한다고 생각해봅니다. 갈라진 곳은 100.5\(m^2\)입니다. 의사결정 트리 모델을 사용하는 주택 가격 추정기를 사용하는 사용자의 입장에서 생각해봅니다. 그들은 자신의 집에 대한 정보를 측정해서 그 집이 99\(m^2\)라는 결론에 도달해서, 가격 계산기에 입력하더니 2억5천만원이라는 예측을 하게 됩니다. 그런데 2\(m^2\)의 작은 창고를 포함하여 측정하는 것을 깜빡했습니다. 창고에 경사진 벽이 있어 전체 면적으로 할지 절반만 할지 확신하기 어렵게 됩니다. 그래서 사용자는 100.0\(m^2\)와 101.0\(m^2\)를 계산해봅니다. 그 결과 2억5천만원에서 2억6천만원이 계산되는데 이는 직관적이지 않습니다. 왜냐하면 방의 면적 차이가 99\(m^2\)에서 100\(m^2\)로 변한것 밖에 없기 때문입니다.
트리도 상당히 불안정합니다. 학습 데이터 세트의 몇 가지 변경은 완전히 달느 트리를 만들 수 있습니다. 각 분할은 부모 노드의 분할에 따라 다르기 때문입니다. 그리고 다른 특성값을 첫 번째 분할 특성값으로 선택하면 전체 트리 구조가 바뀝니다. 구조가 그렇게 쉽게 바뀌면 모델에 대한 신뢰도를 형성할 수 없게 됩니다.
의사결정 트리는 트리가 매우 짧을 경우 해석이 너무 쉬워집니다. 깊이가 깊어질수록 말단 노드의 갯수는 빠르게 증가합니다. 말단 노드가 많고 트리가 깊을수록 트리의 의사결정 규칙을 이해하기 어려워집니다. 1의 깊이는 2개의 말단 노드를 의미합니다. 깊이 2는 최대 4개의 노드를 의미합니다. 깊이 3은 최대 8개 노드를 의미합니다. 트리에서 최대 말단 노드 수는 (\(깊이^2\))입니다.
참고자료: https://christophm.github.io/interpretable-ml-book/tree.html
4.4 Decision Tree | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 4. 해석할 수 있는 모델' 카테고리의 다른 글
| [해석할 수 있는 기계학습(4-6)] 룰핏(RuleFit) (0) | 2020.03.01 |
|---|---|
| [해석할 수 있는 기계학습(4-5)] 의사결정 규칙(Decision Rule) (0) | 2020.02.24 |
| [해석할 수 있는 기계학습(4-3)] GLM, GAM 및 상호작용 (3) | 2019.12.26 |
| [해석할 수 있는 기계학습(4-2)] 로지스틱 회귀 (0) | 2019.12.24 |
| [해석할 수 있는 기계학습(4-1)] 선형 회귀 (0) | 2019.12.06 |




