늦깎이 공대생의 인공지능 연구실
[해석할 수 있는 기계학습(4-5)] 의사결정 규칙(Decision Rule) 본문
[해석할 수 있는 기계학습(4-5)] 의사결정 규칙(Decision Rule)
Justin T. 2020. 2. 24. 01:19
의사결정 규칙은 조건(antecedent)과 예측으로 구성된 단순한 IF-THEN 문입니다. 예를 들어 오늘 비가 오고 4월(조건)이면 내일 비가 올 것이다(예상) 와 같은 가정과 같이 말이지요. 이와 같이 단일 결정 규칙 또는 여러 규칙의 조합을 사용하여 예측할 수 있다는 것이 바로 의사결졍 규칙입니다.
의사결정 규칙은 다음과 같은 일반적인 구조와 같습니다. 만약 조건이 THEN을 만족한다면 특정한 예측을 합니다. 의사결정 규칙은 아마도 가장 해석 가능한 예측 모델일 것입니다. IF-THEN 구조는 의미적으로 자연어와 우리가 생각하는 방식과 유사하며, 그 조건이 이해할 수 있는 특징으로부터 만들어 진다면, 조건의 길이는 짧고(소수의 feature=value와 결합된 값 쌍) 규칙도 그리 많지 않습니다. 프로그래밍에서는 IF-THEN 규칙을 쓰는 것이 매우 자연스럽습니다. 기계학습의 새로운 점은 의사결정 규칙이 알고리즘을 통해 학습된다는 것입니다.
집값을 예측하기 위한 결정을 학습하기 위한 알고리즘을 사용한다고 가정해봅니다.(low, medium, high). 이 모델에 의해 학습된 한 가지 의사결정 규칙은, 만약 집이 \(100m^2\)보다 크고 정원이 딸려있으면 집값의 가치는 높아집니다. 이는 다시 말해 아래와 같이 표현할 수 있겠습니다.
IF
size>100 AND garden=1;
THEN
value=high
이번에는 위에서 언급하였던 의사결정 규칙은 세분화해봅니다.
-
size>100은 IF의 첫 번째 조건입니다.
-
garden=1은 IF의 두 번째 조건입니다.
-
위의 두 조건은 'AND'로 연결하여 새로운 조건을 만듭니다. 여기서 두 가지가 동시에 만족되어야 합니다.
-
THEN에서 value=high는 예상되는 결과입니다.
의사결정 규칙은 적어도 하나의 조건으로 feature=value을 사용하며 'AND'의 갯수는 제한을 두지 않습니다. 한 가지 예외로 명시적인 IF가 없고 다른 규칙이 적용되지 않을 때엔 기본 규칙대로 진행됩니다.
유용한 결정 규칙은 서포트(Support)와 정확도(Accuracy) 두 가지로 요약됩니다.
1. 규칙의 서포트 혹은 범위
규칙의 조건이 적용되는 인스턴스의 비율을 서포트(Support)라고 합니다. 집값을 예측하기 위해 다음과 같은 규칙이 있다고 가정해봅니다.
size=big AND location=good THEN value=high
1000채의 집 중 100채가 크고 좋은 위치에 있다고 가정하면, 그 규칙의 서포트(Support)는 10%라 할 수 있습니다. 예측(THEN)은 서포트의 계산에 중요하지 않습니다.
2. 규칙의 정확도 혹은 신뢰도
규칙의 정확도는 규칙의 조건이 적용되는 인스턴스에 대한 올바른 클래스를 예측하는 데 있어서 규칙이 얼마나 정확한지를 나타내는 척도입니다. 100마리의 말이 있다고 가정해 봅시다.
size=big AND location=good THEN value=high
85마리가 value=high이고 14마리가 value=medium이고 1마리가 value=low일 때 이 규칙의 정확도는 85%입니다.
보통 정확도와 서포트 사이의 절충점이 있습니다. 조건에 더 많은 특성값을 추가함으로서 더 높은 정확도를 잘성할 수 있지만 서포트를 잃을 수 있습니다.
집값을 예측하기 위한 좋은 분류방법을 만들기 위해서는 하나의 규칙뿐만 아니라 아마도 10~20가지 규칙을 배워야 할 것입니다. 그러면 이것이 더 복잡해질 수 있고 다음 문제들 중 한 가지와 충돌할 수 있습니다.
-
규칙이 겹치는 경우: 만약 집값을 예측하기 위해 두 개 이상의 규칙이 적용되었을 때 모순된 예측을 하게 된다면?
-
적용되는 규칙이 없는 경우: 만약 집값을 예측하고 싶은데 그 어떤 규칙도 적용되지 않는다면?
여러 규칙을 결합하는 두 가지 주요 전략으로 의사결정 목록(순차) 및 의사결정 집합(비순차)가 있습니다. 두 전략 모두 중복되는 규칙 문제에 대한 다른 해결책을 갖고 있습니다.
의사결정 목록(decision list)은 의사결정 규칙에 순서를 부여합니다. 예를 들어 첫 번째 규칙의 조건이 사실이라면 첫 번째 규칙의 예측을 사용합니다. 그렇지 않으면 다음 규칙으로 이동한 다음 적용 여부 등을 확인합니다. 의사결정 목록은 적용되는 목록에서 첫 번째 규칙의 예측만 return하여 중복 규칙 문제를 해결합니다.
의사결정 집합(decision set)은 일부 규칙이 더 높은 투표권을 가질 수 있다는 점을 제외하고는 규칙의 민주주의와 유사합니다. 집합에서 규칙은 상호 배타적이거나, 개별 규칙 정확도나 기타 개별 규칙 정확도나 기타 품질 척도에 의해 가중될 수 있는 다수결 등의 갈등 해결 전략이 있습니다. 해석력은 몇 가지 규칙이 적용될 때 잠재적으로 어려움을 겪습니다.
의사결정 목록과 집합 모두 한 인스턴스에 규칙이 적용되지 않는 문제를 겪을 수도 있습니다. 이것은 기본 규칙을 도입하여 해결할 수 있습니다. 기본 규칙은 다른 규칙이 적용되지 않을 때 적용되는 규칙입니다. 기본 규칙의 예측은 다른 규칙에서 다루지 않는 데이터 포인트의 가장 빈번한 클래스인 경우가 많습니다. 규칙 집합이나 목록이 전체 feature space를 포함될 때 규칙이 완전하다고 볼 수 있습니다. 기본 규칙을 추가함으로서 의사결정 집합 혹 의사결정 목록이 자동으로 완전해집니다.
데이터로부터 규칙을 배우는 방법은 굉장히 많으며 이를 모두 다루기는 어렵습니다. 여기서는 그 중 세 가지를 보이고자 합니다. 알고리즘은 학습 규칙을 위한 광범위한 일반적인 아이디어를 다루기 위해 선택되므로, 세 가지 알고리즘은 모두 매우 다른 접근 방식을 나타냅니다.
1. OneR
OneR은 단일 특성값에서 규칙을 학습합니다. OneR은 단순성, 해석력과 이 둘에 대한 벤치마크로서의 사용이 특징입니다.
2. 순차적 적용(Sequential covering)
순차적 적용(Sequential covering)은 규칙을 반복적으로 학습하고 새로운 규칙에서 다루는 데이터 포인트를 제거하는 일반적인 절차입니다. 이 절차는 많은 규칙 학습 알고리즘에 의해 사용됩니다.
3. 베이즈 규칙 목록(Bayesian Rule Lists)
Bayesian Rule List는 미리 채굴된 빈번한 패턴을 베이시안 통계를 사용하여 의사결정 목록으로 결합합니다. 미리 채굴된 패턴을 사용하는 것은 많은 규칙 학습 알고리즘에 의해 사용되는 일반적인 접근 방식입니다.
이들 중 가장 간단한 접근방법은 OneR부터 알아보도록 하겠습니다.
단일 특성값에서 규칙 학습(OneR)
Holte(1993)가 제안한 OneR 알고리즘은 가장 단순한 규칙 유도 알고리즘 중 하나입니다. 모든 특성값에서 OneR은 관심 결과에 대한 가장 많은 정보를 전달하는 특성값을 선택하고 이 특성값에서 의사결정 규칙을 만듭니다.
"One Rule"을 나타내는 OneR이라는 이름에도 불구하고, 알고리즘은 두 개 이상의 규칙을 생성합니다. 이는 실제로 선택된 최고 특성값의 고유한 특성값당 하나의 규칙입니다.
이 알고리즘은 간단하고 빠른 특징을 가지고 있습니다.
- 적절한 간격을 선택하여 연속된 특성값을 별개의 것으로 이산화시킵니다.
- 각 특성값에 대하여
- 특성값과 (카테고리) 결과값 사이에 교차 테이블을 만듭니다.
- 특성값의 각 값에 대해 이 특정한 특성값이 있는 인스턴스의 가장 빈번한 클래스를 예측하는 규칙을 생성합니다.(크로스 테이블에서 읽을 수 있습니다).
- 특성값에 대한 규칙의 총 오류를 계산합니다. - 총 오류가 가장 작은 특성값을 선택합니다.
OneR은 선택한 특성값의 모든 레벨을 사용하기 때문에 항상 데이터 세트의 모든 인스턴스를 다룹니다. 누락된 값은 추가 특성값으로 처리하거나 미리 귀속시킬 수 있습니다.
OneR 모델은 분할이 하나만 있는 의사결정 트리입니다. 분할은 반드시 CART와 같이 2진수일 필요는 없지만 고유한 특성값의 수에 따라 달라집니다.
OneR에 의해 가장 좋은 특성값이 선택되는 예를 들어봅시다. 아래의 표는 가치, 위치, 크기 및 애완동물 허용 여부에 대한 정보를 포함하는 주택에 대한 인공 데이터 세트를 보여줍니다. 집값을 예측하는 간단한 모델을 배우는 것에 목표를 두고 살펴봅니다.
| location | size | pets | value |
| good | small | yes | high |
| good | big | no | high |
| good | big | no | high |
| bad | medium | no | medium |
| good | medium | only cats | medium |
| good | small | only cats | medium |
| bad | medium | yes | medium |
| bad | small | yes | low |
| bad | medium | yes | low |
| bad | small | no | low |
OneR은 각 특성값과 결과 사이에 크로스테이블을 생성합니다.
value=low value=medium value=high
| value=low | value=medium | value=high | |
| location=bad | 3 | 2 | 0 |
| location=good | 0 | 2 | 3 |
| value=low | value=medium | value=high | |
| size=big | 0 | 0 | 2 |
| size=medium | 1 | 3 | 0 |
| size=small | 2 | 1 | 1 |
| value=low | value=medium | value=high | |
| pets=no | 1 | 1 | 2 |
| pets=only cats | 0 | 2 | 0 |
| pets=yes | 2 | 1 | 1 |
각 특성값에 대해 각 특성값은 규칙의 IF 부분이며, 이 특성값을 가진 인스턴스의 가장 일반적인 클래스는 규칙의 THEN 부분입니다. 예를 들어, size에 대한 특성값으로 small, medium, big과 같은 세 가지 레벨이 있습니다. 각 특성값에 대해 생성된 규칙의 총 오류(오차의 합)을 계산합니다. Location 특성값은 긍정적인 값은 good과 부정적인 값인 bad가 있습니다. 좋지 않은 곳에 있는 주택의 가치가 가장 빈번한 것은 low이며, low를 예측으로 사용할 때, 두 개의 집이 medium 가치를 갖고 있기 때문에 두 개의 실수가 발생합니다. 좋은 위치에 있는 집의 예측 가치는 high이고 여기서 또 다시 두 개의 실수를 저지르게 됩니다. 왜냐하면 두 집은 medium의 가치를 가지고 있기 때문입니다. location 특성값을 사용하였을 때 발생하는 오류는 4/10이며, size 특성은 3/10이고, pets 특성은 4/10입니다. size 특성은 가장 낮은 오류로 규칙을 생성하며 아래 세 번째 OneR 모델이 사용될 것입니다.
IF size=small THEN value=small
IF size=medium THEN value=medium
IF size=big THEN value=high
OneR은 가능한 레벨이 많은 특성값을 선호하는데, 그러한 특성값은 목표값에 더 쉽게 맞출 수 있기 때문입니다. 모든 특성값이 무작위 값을 취하고 목표값에 대한 예측값이 없음을 의미하는, 노이즈만 포함하고 신호는 없는 데이터 세트를 가정해봅니다. 몇몇 특성값들은 다른 것들보다 더 많은 수준을 가지고 있습니다. 레벨이 더 높은 특성값이 이제 더 쉽게 오버피트가 될 수 있습니다. 데이터에서 각 인스턴스에 대해 별도의 레벨이 있는 특성값은 전체 학습 데이터셋을 완벽하게 예측할 수 있습니다. 이에 대한 해결책은 데이터를 학습 및 검증 세트로 나누고, 학습 데이터에 대한 규칙을 학습하고, 검증 세트의 특성값을 선택하는 총 에러를 평가하는 것입니다.
Tie는 또 다른 이슈로, 즉 두 특성값이 동일한 총 에러를 야기할 때 발생합니다. OneR은 오류가 가장 낮은 첫 번째 특성값을 취하거나 카이 제고 테스트의 p-value값이 가장 낮은 특성값을 취함으로서 tie를 해결합니다.
예제
실제 데이터를 활용하여 OneR을 사용해봅니다. OneR 알고리즘을 테스트하기 위해 자궁경부암 분류 작업을 사용해봅니다. 모든 연속 입력 특성값은 5개로 구분되어 다음과 같은 규칙을 생성합니다.
| Age | prediction |
| (12.9,27.2] | Healthy |
| (27.2,41.4] | Healthy |
| (41.4,55.6] | Healthy |
| (55.6,69.8] | Healthy |
| (69.8,84.1] | Healthy |
연령 특성값은 OneR에 의해 가장 좋은 예측 특성값으로 선택되었습니다. 암에 걸리는 경우는 드물기 때문에, 각 규칙에서 대다수의 레벨과 예측된 label은 항상 건강하기 때문에 다소 도움이 되지 않습니다. 이 불균형한 경우에 label 예측을 사용하는 것은 말도 안됩니다. 암에 걸린 여성의 비율과 함께 'Age' 간격과 Cancer/Healty 사이의 크로스테이블이 더 이해하는데 좋은 듯 합니다.
| # Cancer | # Healthy | P(Cancer) | |
| Age=(12.9,27.2] | 477 | 26 | 0.95 |
| Age=(27.2,41.4] | 290 | 25 | 0.92 |
| Age=(41.4,55.6] | 31 | 4 | 0.89 |
| Age=(55.6,69.8] | 1 | 0 | 1.00 |
| Age=(69.8,84.1] | 4 | 0 | 1.00 |
그러나 어떤 것을 해석하기 전에 모든 특성값과 모든 값에 대한 예측이 정상적으로 나타나고 있기 때문에, 전체 오류율은 모든 특성값에 대해 동일합니다. 총 오류에서 tie는 기본적으로 오류율이 가장 낮은 특성값의 첫 번째 특성값을 사용하여 해결되며(여기서는 모든 특성값이 55/858), 이는 우연히 Age 특성값이 됩니다.
OneR은 회귀 작업을 지원하지 않습니다. 그러나 연속적인 결과를 간격으로 잘라냄으로써 회귀 과제를 분류 과제로 바꿀 수 있습니다. 자전거의 수를 4가지(0-25%, 25-50%, 50-75%, 75-100%)로 줄여서 OneR과 함께 대여한 자전거의 수를 예측하기 위해 이러한 방법을 사용합니다. 아래의 표는 OneR 모델을 통해 나타나는 특성값을 나타냅니다.
| mnth | prediction |
| JAN | [22,3152] |
| FEB | [22,3152] |
| MAR | [22,3152] |
| APR | (3152,4548] |
| MAY | (5956,8714] |
| JUN | (4548,5956] |
| JUL | (5956,8714] |
| AUG | (5956,8714] |
| SEP | (5956,8714] |
| OKT | (5956,8714] |
| NOV | (3152,4548] |
| DEZ | [22,3152] |
여기서 선택한 특성값은 월단위 입니다. 월별 특성값은 놀랍게도 대부분의 다른 특성값보다 많은 12가지 특성값 레벨을 갖고 있습니다. 그래서 오버피팅의 위험이 존재합니다. 좀 더 낙관적은 관점에서 본다면 월별 특성값은 계절적 추세(예를 들어 겨울에 임대된 자전거의 대수가 적은 경우)를 처리할 수 있으며 이러한 예측은 합리적으로 보입니다.
다음으로 간단한 OneR 알고리즘에서 다음과 같은 여러 가지 특성값으로 구성된 보다 복잡한 조건을 가진 규칙을 사용하여 보다 복잡한 절차인 순차적 적용(Sequential Covering)에 다루어 보겠습니다.
2. 순차적 적용(Sequential Covering)
순차적 적용은 규칙별로 전체 데이터 집합 규칙을 다루는 의사결정 목록(혹은 집합)을 작성하기 위해 단일한 규칙을 반복적으로 학습하는 일반적인 절차입니다. 규칙 학습 알고리즘은 순차적 적용 알고리즘의 변형이기도 합니다. 여기서는 주요 방안들을 소개하고 예제를 위한 순차적 적용 알고리즘의 변형은 RIPPER을 사용해보고자 합니다.
아이디어는 간단합니다. 먼저 데이터 포인트 중 일부에 적용되는 올바른 규칙을 찾아냅니다. 규칙에서 예외 처리를 할 수 있는 모든 데이터 포인트를 제거합니다. 데이터 포인트는 포인트가 정확하게 분류되는지 여부에 관계없이 조건이 다루어질 때 적용됩니다. 더 이상의 포인트가 남지 않거나 다른 정지 조건이 충족될 때 까지 나머지 포인트로 적용된 포인트의 규칙 학습 및 제거를 반복합니다. 그 결과는 의사결정 목록이 됩니다. 적용된 데이터 포인트의 반복적인 규칙 학습 및 제거 접근 방식을 "분리 및 조정(separate-and-conquer)"라고 합니다.
데이터의 일부를 포함하는 단일 규칙을 만들 수 있는 알고리즘을 가지고 있다고 가정해봅니다. 두 클래스(양수, 음수)에 대한 순차적 적용 알고리즘은 다음과 같이 작동합니다.
- 초기화된 빈 규칙 목록(rlist)부터 시작합니다.
- 규칙 r을 학습합니다.
- 규칙 목록이 특정 임계값 미만일 경우(또는 양수로 분류되지 않는 경우)
- r을 rlist에 추가합니다.
- 규칙 r에 의해 처리된 모든 데이터 포인트를 삭제합니다.
- 남아있는 데이터로 또다른 규칙을 학습힙니다. - 의사결정 리스트를 return합니다.
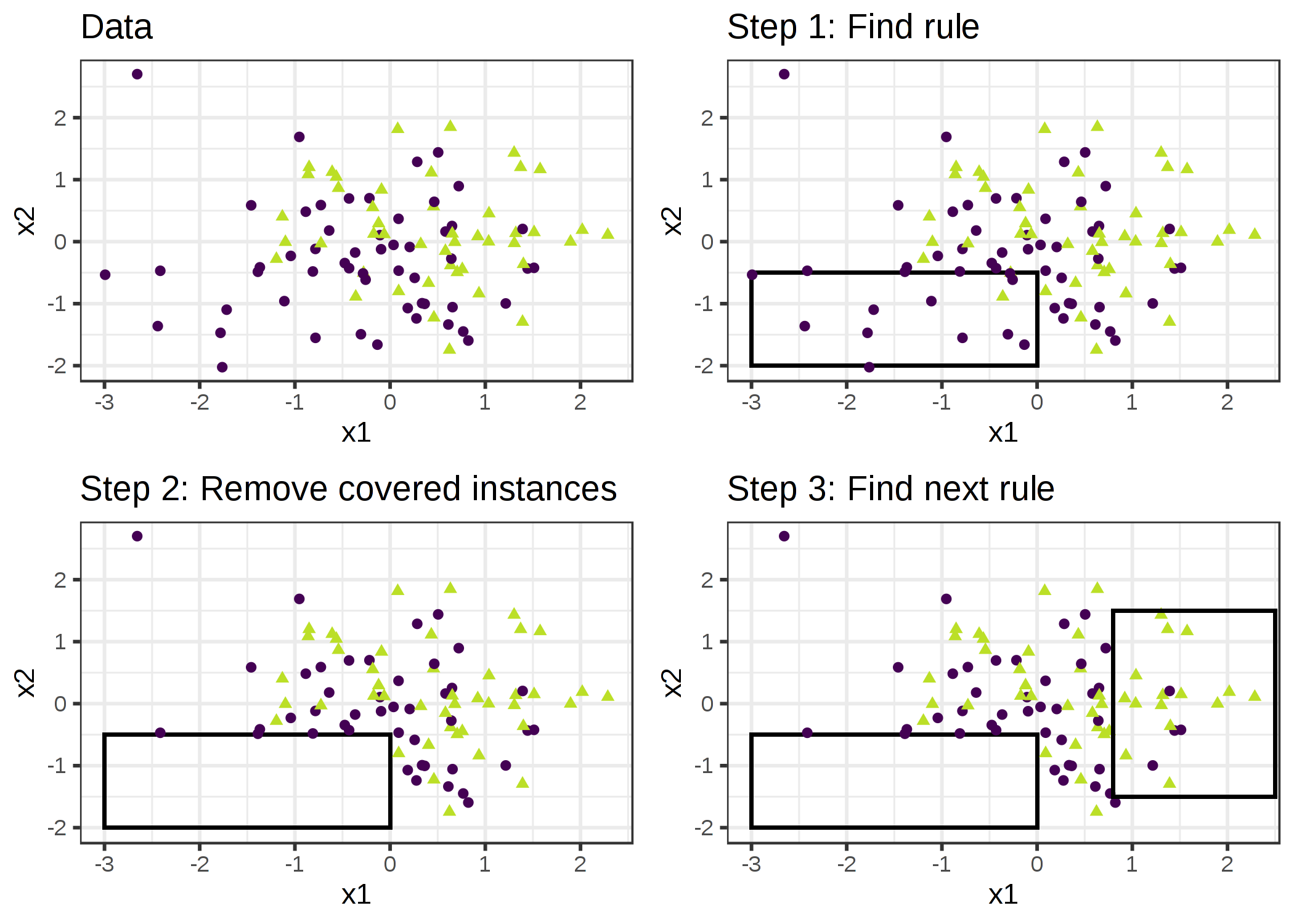
예를 들어 크기와 위치, 애완동물 허용 여부 등 집값을 예측하는 작업과 데이터셋을 가지고 있을 때, 첫 번째 규칙을 배웁니다.
IF size=big AND location=good, THEN value=high
이 규칙을 통해 데이터셋에서 location이 good이고 size가 big인 데이터를 삭제합니다. 그런 다음 남아있는 데이터들을 가지고 다음과 같은 규칙을 배웁니다.
IF location=good, THEN value=medium
이 규칙은 좋은 위치에 큰 집이 없는 데이터에서 학습되어 중간 크기의 집과 작은 크기의 집만 좋은 장소에 있다는 점을 주목해볼만 합니다.
다중 클래스 설정의 경우, 접근 방식을 수정해야 합니다. 먼저, 각 클래스들을 유입을 증가시킴으로서 순서를 정해줍니다. 순차적 적용 알고리즘은 가장 낮은 공통 클래스로 시작하고, 규칙을 학습하고, 처리된 인스턴스를 모두 제거한 다음, 두 번째로 가장 작은 공통 클래스로 이동시킵니다. 현재의 클래스는 항상 양수 클래스로 취급되고, 가장 유입이 많은 모든 클래스는 음수 클래스로 결합됩니다. 마지막 클래스가 기본 규칙이 됩니다. 이는 분류방법에 있어 일대다 전략이라고도 합니다.
그렇다면 어떻게 단일한 규칙을 배울 수 있을까요? OneR 알고리즘은 항상 전체 특성 공간을 포함하므로 여기서는 그다지 쓸모업게 됩니다. 그러나 다른 많은 가능성들이 있습니다. 하나의 가능성은 beam search를 사용하는 의사결정 트리에서 단일 규칙을 배우는 방법입니다.
- 의사결정 트리(CART 혹은 다른 트리 학습 알고리즘 포함)을 학습합니다.
- Root 노드에서 시작하여 가장 순수한 노드(가장 낮은 오분류율)를 재귀적으로 선택합니다.
- 말단 노드의 다수의 클래스는 규칙 예측으로 사용되며, 해당 노드로 이어지는 경로는 규칙 조건으로 사용됩니다.
아래의 그림은 트리에서 beam 서치를 설명하는 그림입니다.
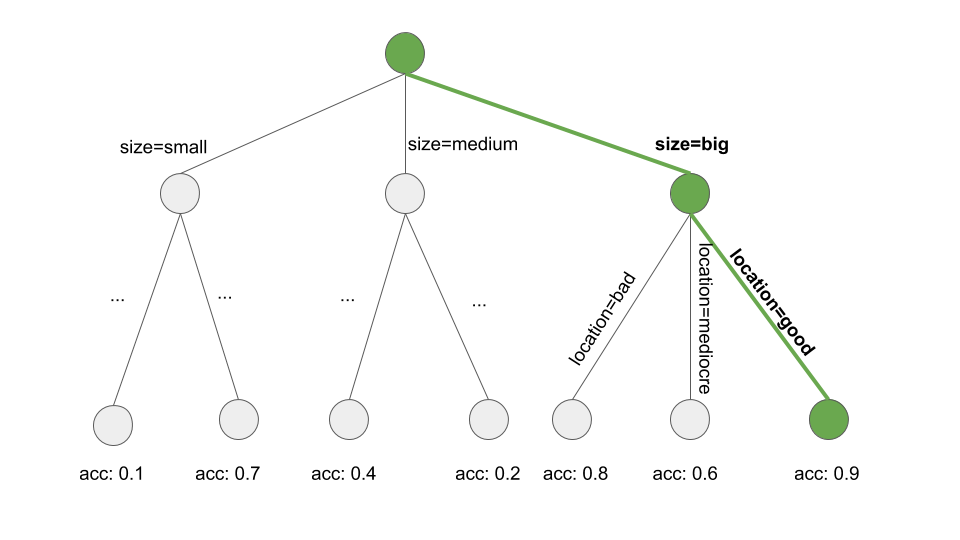
단일 규칙을 배우는 것은 탐색의 문제인데, 여기서 탐색 공간은 가능한 모든 규칙의 공간입니다. 탐색의 목표는 어떤 기준에 따라 최선의 규칙을 찾는 것입니다. 이러한 탐색에는 다양한 전략들이 있습니다. 대표적인 것으로 beam 탐색, hill-climbing(언덕오르기), 완전 탐색, 최상우선 탐색, ordered 탐색, stochastic search(확률에 의한 탐색), top-down search(하향식 탐색), bottum-up search(상향식 탐색)등이 있습니다.
Cohen(1995)이 제안한 RIPPER(Repeated Incremental Pruning to Produce Error Reduction)는 순차적 적용 알고리즘의 변형입니다. RIPPER는 좀 더 정교하고 사후 처리 단계(규칙 가지치기)를 사용하여 의사결정 목록(혹은 세트)을 최적화합니다. RIPPER는 순서 또는 순서가 없는 모드로 실행될 수 있으며 의사결정 목록 또는 의사결정 집합을 생성합니다.
예제
예제로 RIPPER를 사용해봅니다. 안타깝게도 RIPPER 알고리즘은 자궁경부암의 분류 작업에서 그 어떤 규칙도 찾아내지 못합니다.
회귀 작업에서 RIPPER를 사용하여 자전거 대여수를 예측할 때 몇 가지 규칙이 발견됩니다. RIPPER는 분류를 위해서만 작동하기 때문에 자전거 대여수는 반드시 카테고리형 결과로 변경되어야 합니다. 이는 자전거의 숫자를 4분위로 줄임으로서 해결할 수 있습니다. 예를 들어 (4548, 5956)은 4548개에서 5956개 사이의 예상 자전거 대여수를 포함하는 구간입니다. 아래의 표는 학습된 규칙의 의사결정 목록을 나타냅니다.
| rules |
| (days_since_2011 >= 438) and (temp >= 17) and (temp <= 27) and (hum <= 67) => cnt=(5956,8714] |
| (days_since_2011 >= 443) and (temp >= 12) and (weathersit = GOOD) and (hum >= 59) => cnt=(5956,8714] |
| (days_since_2011 >= 441) and (windspeed <= 10) and (temp >= 13) => cnt=(5956,8714] |
| (temp >= 12) and (hum <= 68) and (days_since_2011 >= 551) => cnt=(5956,8714] |
| (days_since_2011 >= 100) and (days_since_2011 <= 434) and (hum <= 72) and (workingday = WORKING DAY) => cnt=(3152,4548] |
| (days_since_2011 >= 106) and (days_since_2011 <= 323) => cnt=(3152,4548] |
| => cnt=[22,3152] |
위 표의 해석은 간단합니다. 만약 조건이 적용된다면, 자전거의 수에 대한 우측의 간격을 예측합니다. 마지막 규칙은 인스턴스에 적용되는 다른 규칙이 없을 때 적용되는 기본 규칙입니다. 새로운 인스턴스를 예측하려면 목록 맨 위에서 시작하여 규칙이 적용되는지의 여부를 확인합니다. 조건이 일치하면 규칙의 오른쪽은 이 인스턴스에 대한 예측입니다. 기본 규칙은 항상 예측이 존재하도록 보장합니다.
3. 베이즈 규칙 목록(Bayesian Rule Lists)
여기서부터는 의사결정 목록을 학습하기 위한 또 다른 접근 방식을 보여드리겠습니다. 이 방법은 다음과 같이 진행됩니다.
- 의사결정 규칙의 조건으로 사용할 수 있는 데이터로부터 빈번한 패턴을 미리 파악한다.
- 미리 지정된 규칙의 선택 항목에서 의사결정 목록을 학습합니다.
위의 방법을 사용하는 구체적인 접근법을 베이즈 규칙 목록(Letham et. al, 2015) 또는 BRL이라고 합니다. BRL은 베이즈 통계를 사용하여 FP-tree 알고리즘(Borgelt, 2005)으로 미리 채굴된 빈번한 패턴에서 의사결정 목록을 학습하는 것입니다.
BRL의 첫 단계부터 천천히 알아보도록 하겠습니다.
빈번한 패턴의 사전 채굴(Pre-mining)
빈번한 패턴은 특성값의 빈번한 (동시)발생을 의미합니다. BRL 알고리즘의 사전 처리단계로서, 특성값을 사용하고(이 단계에서 목표값의 결과가 필요하지 않음) 그것들로부터 자주 발생하는 패턴을 추출합니다. 패턴은 size=medium과 같은 단일 특성값 또는 size=medium AND location=bad와 같은 특성값의 조합이 될 수 있습니다.
패턴의 빈도는 데이터셋의 값으로부터 측정됩니다.
$$Support(x_j=A)=\frac{1}n{}\sum_{i=1}^nI(x^{(i)}_{j}=A)$$
여기서 A는 특성값이며, n은 데이터셋이 가지고 있는 데이터 포인트의 갯수를 나타내며, \(I\)는 인스턴스 i의 특성값 \(x_j\)가 레벨 A일 경우 1을 반환하고 그렇지 않을 경우 0을 반환하는 척도(Indicator)함수입니다. 집값의 데이터 집합에서, 20%의 집들이 발코니가 없고 80%가 하나 이상의 집을 가지고 있다면, 패턴 balcony=0에 대한 서포트(Support)는 20%입니다. 또한 특성값의 조합 balcony=0 AND pets=allowed에 대해서도 서포트를 측정할 수 있습니다.
빈번한 패턴을 찾기 위한 알고리즘은, 예를 들어 연관규칙(Apriori)알고리즘이나 FP-Growth 알고리즘과 같은 여러가지가 있습니다. 어떤 것을 사용하는지는 별로 중요하지 않습니다만, 패턴을 찾아내는 속도에서 차이가 날 뿐, 결과적인 패턴은 항상 같습니다.
Apriori 알고리즘이 어떻게 작동되어 빈번한 패턴을 찾는지 대략적으로 다음과 같습니다. 실제로 Apriori 알고리즘은 두 부분으로 구성되어 있는데, 먼저 빈번한 패턴을 발견하고 다음에는 그러한 것들로부터 연관된 규칙을 만듭니다. BRL 알고리즘의 경우, Apriori의 첫 부분에서 생성되는 빈번한 패턴에 초점이 맞추어져 있습니다.
첫 번째 단계에서 Apriori 알고리즘은 사용자가 정의한 최소 서포트보다 큰 서포트를 가진 모든 특성값으로부터 시작합니다. 사용자가 최소 서포트가 10%이고 단 5%의 집만이 size=big라는 특성값을 갖고 있을 때, 우리는 패턴에서 size=big라는 값만 제거한 후 size=medium과 size=small만을 남겨둡니다. 이는 해당되는 집들이 데이터에서 제거되었다는 것을 의미하는 것이 아니라 단지 size=big라는 특성값이 빈번한 패턴으로 반환되지 않는다는 것을 의미합니다. 단일 특성값의 빈번한 패턴을 기반으로 Apriori 알고리즘은 반복적으로 점점 더 높은 수준의 특성값의 조합을 찾으려고 합니다. 패턴은 항상 feature=value 라는 판단과 논리 AND(예를 들어 size=medium AND location=bad)를 결합하여 구성합니다. 최소 서포트보다 낮은 서포트를 가진 생성된 패턴은 제거됩니다. 결국 모든 빈번한 패턴을 갖게 된다는 것이지요. 빈번한 패턴의 어떤 부분집합도 다시 빈번하게 발생하는데, 이것을 Apriori 속성이라고 합니다. 이는 직관적으로 타당하다고 볼 수 있습니다. 패턴에서 조건을 제거함으로써, 감소된 패턴은 더 많은 또는 같은 수의 데이터 포인트만 포함할 수 있을 뿐이지, 더 적어지지는 않는다는 것입니다. 예를 들어, 주택의 20%가 size=medium AND location=good일 때, size=medium만 있는 주택의 서포트는 20% 이상입니다. Apriori 속성은 검사할 패턴의 수를 줄이기 위해 사용됩니다. 빈번한 패턴에 대해 더 높은 순위의 패턴을 확인해야 합니다.
이제 베이즈 규칙 목록 알고리즘의 채굴 전 조건을 모두 마쳤습니다. 그러나 BRL의 두 번째 단계로 넘어가기 전에 미리 채굴된 패턴을 기반으로 한 규칙 학습의 다른 방법에 대한 힌트를 주고자 합니다. 다른 접근방식은 빈번한 패턴 채굴 프로세스에 원하는 결과값을 포함시키고 IF-THEN 규칙을 만드는 Apriori 알고리즘의 두 번째 방법으로 넘어가는 것을 제안하고자 합니다. 왜냐하면 이 알고리즘은 비지도학습이기 때문에 THEN 부분에서는 관심이 없는 특성값도 포함되어 있습니다. 그러나 오직 원하는 결과만을 가지고 있는 규칙으로 필터링할 수 있습니다. 이러한 규칙은 이미 결정 집합을 구성하지만, 규칙을 나란히 배열하거나, 잘라내거나, 삭제하거나, 다시 결합된것일수도 있습니다.
그러나 BRL 접근법에서는 빈번한 패턴으로 작업하며, THEN 및 그 패턴을 베이즈 통계를 사용하여 의사결정 목록으로 배열하는 방법을 배우고자 합니다.
베이즈 규칙 목록 학습
BRL 알고리즘의 목표는 미리 채굴한 조건의 선택을 이용하여 정확한 의사결정 목록을 학습하는 동시에, 규칙과 조건이 적은 목록의 우선순의를 정하는 것입니다. BRL은 조건의 길이(우선적으로 더 짧은 규칙)와 규칙의 수(최소한 더 짧은 목록)에 대한 사전 분포와 함께 의사결정 목록의 분포를 정의함으로써 이루어지는 목표를 설명하고자 합니다.
목록의 사후(posteriori) 확률 분포를 통해 결정의 가능성과 목록이 데이터에 얼마나 잘 맞는지 가정할 수 있습니다. 사후 확률을 최대화 하는 목록을 찾는 것이 목표입니다. 목록의 분포에서 직접 가장 적합한 목록을 찾을 수 없기 때문에 BRL은 아래와 같은 방법을 제안합니다.
- 사전 분포(Priori distribution)에서 무작위로 추출한 최초 의사결정 목록을 생성한다.
- 규칙의 추가, 전환 또는 삭제함으로서 리스트를 반복적으로 수정하고, 그 결과 목록이 목록의 사후 분포(Posterior distribution)를 따르도록 합니다.
- 사후 분포에 따라 확률이 가장 높은 샘플링된 목록에서 의사결정 목록을 선택합니다.
베이즈 규칙 목록 알고리즘을 좀 더 자세히 살펴보도록 합시다. 베이즈 규칙 목록 알고리즘은 FP-growth 알고리즘을 사용하여 특성값 패턴을 미리 채굴하는 것으로 시작합니다. BRL은 목표값의 분포와 그 분포를 정의하는 매개변수의 분포에 대해 여러가지 가정을 합니다.(이를 베이즈 통계량이라 합니다.) 베이즈 통계에 대해 익숙하지 않더라도 다음 설명에 대해 너무 얽메이지 않으셔도 됩니다. 베이즈 접근 방식은 기존 지식이나 요구사항(사전 분포)을 겹합하는 동시에 데이터에 적합하다는 것을 아는 것이 중요합니다. 의사결정 목록의 경우, 이전의 가정은 의사결정 목록을 짧은 규칙으로 요약하기 때문에 베이즈 접근법은 타당하다고 볼 수 있습니다.
사후 분포로부터 의사결정 목록 d를 샘플링하는 것을 목표로 하였을 때
$$\underbrace{p(d|x,y,A,\alpha,\lambda,\eta)}_{posteriori}\propto\underbrace{p(y|x,d,\alpha)}_{likelihood}\cdot\underbrace{p(d|A,\lambda,\eta)}_{priori}$$
여기서 d는 의사결정 목록, x는 특성값, y는 미리 채굴된 조건의 집합, λ는 의사결정 목록의 이전 예상 기간, η은 사전 예상 조건 수, α는 (1,1)에서 가장 잘 고정된 양수 및 음수 클래스에 대한 사전 근사수(pseudo-count)를 의미합니다.
$$p(d|x,y,A,\alpha,\lambda,\eta)$$
관측된 데이터와 사전 가정(Priori assumptions)을 고려할 때 의사결정 목록이 얼마나 개연성이 있는지를 정량화합니다. 이는 의사결정 목록에 주어진 결과 y의 확률에 비례하며, 데이터는 주어진 사전 가정과 미리 채굴된 조건의 목록 확률에 비례합니다.
$$p(y|x,d,\alpha)$$
의사결정 목록과 데이터를 고려할 때 관측된 y의 가능성(likelihood)입니다. BRL은 y가 디리클레 다항분포(Dirichlet-Multinomial Distribution)에 의해 생성된다고 가정합니다. 의사결정 목록 d가 데이터를 더 잘 설명할수록 가능성은 더 높아집니다.
$$p(d|A,\lambda,\eta)$$
이 식은 의사결정 목록의 사전 분포(Priori distribution)를 나타냅니다. 목록의 규칙 수에 대해서는 잘린 포아송 분포(파라미터 λ)와 규칙 조건의 특성값의 갯수에 대해서는 잘린 포아송 분포(파라미터 η)를 곱하여 결합합니다.
의사결정 목록은 결과 y를 잘 설명하고 사전 가정에 따라 가능성이 높은 경우 사후 확률(Posterior probability)이 높습니다.
베이즈 통계에서 추정치를 다루는 것은 약간 까다롭습니다. 왜냐하면 대개 정답을 직접 계산할 수는 없지만, 후보를 뽑고, 평가하고, 마르코프 연쇄 몬테 카를로(Markov chain Monte Carlo) 방법을 사용하여 사후 추정치를 업데이트해야 하기에 그렇습니다. BRL의 창시자들은 먼저 초기 의사결정 목록을 작성한 후 목록의 사후 분배(의사결정 목록의 마르코프 연쇄)에서 의사결정 목록 샘플을 생성하도록 반복적으로 수정할 것을 제안합니다. 결과는 초기 의사결정 목록에 잠재적으로 의존할 수 있기 때문에 다양한 목록을 확인하기 위해 이를 반복하는 것이 좋습니다. 소프트웨어로 구현할 때 보통 기본값은 10배로 잡습니다. 아래의 방법은 초기 의사결정 목록을 작성하는 방법입니다.
- FP-Growh로 패턴을 미리 파악합니다.
- 절단된 포아송 분포에서 목록 길이 매개변수 m을 샘플링합니다.
- 기본적인 규칙의 경우 디레클레 다항 분포(Dirichlet-Multinomial distribution) 매개변수 \(\theta_0\)을 샘플링합니다.
(다른 규칙이 적용되지 않을 때 적용되는 규칙) - For 의사결정 목록 규칙 j=1,…,m, do:
- 규칙 j에 대한 규칙 길이 매개변수 \(l\)(조건의 갯수)를 샘플링합니다.
- 미리 채굴된 조건으로 길이 \(l_j\)의 조건을 샘플링합니다.
- THEN 부분에 대한 디레클레 다항 분포 매개변수 샘플링(규칙이 지정된 목표 결과의 분포에 대한 샘플링)
- For 데이터셋의 각 관측치:
- 먼저 적용되는 의사결정 목록에서 규칙을 찾습니다.(위에서부터 아래로).
- 적용되는 규칙에 의해 제안된 확률 분포(이항 분포)에서 예측된 결과를 도출합니다.
다음으로 의사결정 목록의 사후분포에에서 많은 표본을 얻기 위해 이 초기 표본부터 많은 새로운 목록을 생성하는 것입니다.
새 의사결정 목록은 초기 목록에서 시작하여 무작위로 목록의 다른 위치로 규칙을 이동하거나 미리 미리 데이터가 채굴된 상태에서 현재 의사결정 목록에 규칙을 추가하거나 제거하는 방식으로 샘플링합니다. 어떤 규칙이 바뀌거나 추가, 또는 삭제되는지 무작위로 선택됩니다. 각 단계에서 알고리즘은 의사결정 목록의 사후 확률을 평가합니다.(정확성과 부족함의 조합). 메트로폴리스-헤이스팅스 알고리즘(Metropolis Hastings Algorithm)은 높은 사후 확률을 가진 의사결정 목록을 표본으로 추출하도록 보장합니다. 이러한 절차는 의사결정 목록의 분산으로부터 많은 표본을 제공합니다. BRL 알고리즘은 가장 높은 사후 확률을 가진 표본의 의사결정 목록을 선택합니다.
예제
이제 BRL 알고리즘을 사용해보도록 합시다. 이 예제에서는 BRL의 더 빠른 변형 알고리즘은 SBRL(Scalable Bayesian Rule Lists)알고리즘(Yang et. al, 2007)을 사용합니다. 자궁경부암의 위험을 예측하기 위해 SBRL 알고리즘을 적용해봅니다. 처음에 SBRL 알고리즘을 동작하기 위해 모든 입력 특성값들을 별개의 것으로 구분하였습니다. 이를 위해 분위수(quantiles)에 의한 값의 빈도를 기반으로 연속된 특성값을 구하였습니다.
다음과 같은 규칙이 있다고 가정해봅니다.
| rules |
| If {STDs=1} (rule[259]) then positive probability = 0.16049383 |
| else if {Hormonal.Contraceptives..years.=[0,10)} (rule[82]) then positive probability = 0.04685408 |
| else (default rule) then positive probability = 0.27777778 |
여기서 우리는 위의 규칙이 합리적인 것을 확인할 수 있습니다. 왜냐하면 위의 예측은 클래스별 결과가 아닌 암에 대한 예측 가능성이기 때문입니다.
조건은 FP-Growth 알고리즘으로 미리 채굴된 패턴에 의해 선택되었습니다. 아래의 표에는 의사결정 목록을 만들기 위해 SBRL 알고리즘이 선택할 수 있는 조건을 나타냅니다. 사용자가 허용하는 조건의 최대 특성값의 최대 갯수는 2개였습니다. 다음은 10가지 패턴의 표본입니다.
| pre-mined conditions |
| Num.of.pregnancies=[3.67,7.33) |
| IUD=0,STDs=1 |
| Number.of.sexual.partners=[1,10),STDs..Time.since.last.diagnosis=[1,8) |
| First.sexual.intercourse=[10,17.3),STDs=0 |
| Smokes=1,IUD..years.=[0,6.33) |
| Hormonal.Contraceptives..years.=[10,20),STDs..Number.of.diagnosis=[0,1) |
| Age=[13,36.7) |
| Hormonal.Contraceptives=1,STDs..Number.of.diagnosis=[0,1) |
| Number.of.sexual.partners=[1,10),STDs..number.=[0,1.33) |
| STDs..number.=[1.33,2.67),STDs..Time.since.first.diagnosis=[1,8) |
다음으로 자전거 대여수의 예측 작업에 SBRL 알고리즘을 적용합니다. 이는 자전거의 갯수 예측의 회귀 문제가 이진 분류 작업으로 변환된 경우에믄 효과가 발생합니다. 자전거 대여수가 하루에 4000대를 초과하면 1이라는 Label을 만들고, 그렇지 않으면 0이라는 분류 작업을 임의로 설정하였습니다.
아래의 목록은 SBRL에 의해 학습된 결과입니다.
| rules |
| If {yr=2011,temp=[-5.22,7.35)} (rule[718]) then positive probability = 0.01041667 |
| else if {yr=2012,temp=[7.35,19.9)} (rule[823]) then positive probability = 0.88125000 |
| else if {yr=2012,temp=[19.9,32.5]} (rule[816]) then positive probability = 0.99253731 |
| else if {season=SPRING} (rule[351]) then positive probability = 0.06410256 |
| else if {yr=2011,temp=[7.35,19.9)} (rule[730]) then positive probability = 0.44444444 |
| else (default rule) then positive probability = 0.79746835 |
2012년 하루동안 17도의 기온일 때 자전거 대여수가 4000대를 넘어설 가능성을 예측해봅니다. 첫 번째 규칙은 2011년 며칠 동안만이므로 적용되지 않고 대신 두 번째 규칙을 적용합니다. 왜냐하면 2012년에 기온이 17도인 날은 [7.35,19.9) 간격에 있기 때문입니다. 4000대 이상의 자전거가 대여될 가능성이 88%라는 것이 이 알고리즘의 예측입니다.
장점
일반적인 IF-THEN 규칙의 장점에 대해 이야기해보겠습니다.
IF-THEN 규칙은 해석하기 쉽습니다. 아마도 가장 해석 가능한 모델일것입니다. 이 표현은 규칙의 수가 적고, 규칙의 조건이 짧고(아마도 최대 3개), 규칙이 의사결정 목록이나 중복되지 않은 결정 집합으로 구성된 경우에만 적용됩니다.
의사결정 규칙은 심지어 더 작은 의사결정 트리처럼 표현될 수 있습니다. 의사결정 트리도 복제된 하위 트리, 즉 왼쪽과 오른쪽 자식 노드의 분할이 동일한 구조를 가질 때 어려움을 겪게됩니다.
IF-THEN 규칙이 적용되는 규칙을 결정하려면 몇 개의 이항 문항만 확인하면 되기 때문에 IF-THEN 규칙을 사용한 예측은 빠릅니다.
의사결정 규칙은 조건의 임계값만 변경되기 때문에 입력 특성값의 단조로운 변환에 대해 강력(Robust)합니다. 이는 또한 어떤 조건이 적용되는 경우에만 문제가 되기 때문에 이상치(Outlier)에 대해 강력합니다.
IF-THEN 규칙은 대개 희박한 모델을 생성하는데, 이는 많은 특성값이 포함되지 않음을 의미합니다. 이 규칙은 모델에 관련된 특징만 선택합니다. 예를 들어, 선형 모델은 기본적으로 모든 입력 특성값에 가중치를 할당합니다. 무관한 특성은 IF-THEN 규칙에 의해 간단히 무시될 수 있습니다.
OneR과 같은 간단한 규칙은 보다 복잡한 알고리즘의 기준으로 사용될 수 있습니다.
단점
일반적인 IF-THEN 규칙의 단점에 대해 살펴보겠습니다.
IF-THEN 규칙에 대한 연구화 문헌은 분류에 초점을 맞추고 있으며 사실상 회귀방법은 고려하지 않습니다. 연속적인 대상을 항상 간격을 나누어 분류 문제로 만들 수 있지만, 항상 정보 손실이 발생합니다. 일반적으로 접근법은 회귀와 분류 모두 사용할 수 있다면 더 매력적입니다.
종종 특성값 또한 카테고리값이어야 합니다. 즉, 수치화된 특성값을 사용하려면 이를 분류해야 합니다. 연속된 특성값을 간격으로 자르는 방법은 여러 가지가 있지만, 이는 사소한 것이 아니며 명확한 답이 없는 많은 의문점이 생깁니다. 특성값을 몇 개의 간격으로 나누어야만 하는 것일까요? 고정된 간격의 길이? 분위수(quantiles)? 혹은 다른 방식의 분할 기준이 존재하는 것일까요? 연속된 특성값을 분류하는 것은 흔히 무시되는 사소하지 않은 문제로서 사람들은 그저 차선책으로 사용합니다.
오래도니 규칙 학습 알고리즘의 대부분은 과적합(overfitting)되기 쉽습니다. 여기서 제시된 알고리즘에는 모두 과적합을 방지하기 위한 최소 몇 가지 안전장치가 있습니다. OneR은 한 가지 특성값만 사용할 수 있기 때문에 사용에 제한되며(특성값이 너무 많은 경우 또는 너무 많은 단계(level)과 같은 많은 특성값이 있는 경우에만 문제됨), RIPPER는 잘라낸 다음 BRL은 의사결정 목록에 사전 분포를 도입합니다.
의사결정 규칙은 특성값과 출력값 사이의 선형 관계를 설명하는데 썩 좋지 못합니다. 이는 의사결정 트리 또한 가지고 있는 문제입니다. 의사결정 트리와 규칙은 단계형 예측 기능만 생산할 수 있는데, 여기서 예측의 변화는 항상 별개의 단계일 뿐 결고 매끄러운 곡선이 아닙니다. 이는 입력 변수가 카테고리화되어야 하는 문제와 연관이 있습니다. 의사결정 트리에서는 이를 분할하여 암묵적으로 분류합니다.
소프트웨어 및 대안
OneR은 R패키지 OneR에 구현되어 있습니다. OneR 또한 웨카(Weka)라는 기계학습 라이브러리에서도 구현되어 Java, R, Python에서도 사용될 수 있습니다. RIPPER 또한 웨카에 구현되어 있습니다. SBRL은 Python 또는 C에서 R패키지로 사용할 수 있습니다.
여기서 의사결정 규칙 집합과 목록에 대해 모두 다루지는 않을 것입니다. 다만 몇 가지 작업을 요약해서 알려드리겠습니다. Fuernkranz et. al(2012)의 "Foundations of Rule Learning"을 추천해드리고자 합니다. 이 책은 의사결정 규칙 집합과 목록에 대해 더 깊이 파고들기를 원하는 사람들을 위해 관련 규칙을 배우는 것에 관한 광범위한 내용을 다룹니다. 학습 규칙을 생각하는 전체적인 틀을 제공하고 많은 규칙 학습 알고리즘에 대해 이해할 수 있습니다. 또한 RIPPER, M5Rules, OneR, PART 등 많은 것을 구현하는 Weka rule learners를 확인해보실 것을 권해드립니다. IF-THEN 규칙은 RuelFit 알고리즘에 대해 설명하는 선형 모델에서 사용할 수 있습니다.
참고자료: https://christophm.github.io/interpretable-ml-book/rules.html
4.5 Decision Rules | Interpretable Machine Learning
Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.
christophm.github.io
'해석할 수 있는 기계학습 > 4. 해석할 수 있는 모델' 카테고리의 다른 글
| [해석할 수 있는 기계학습(4-7)] 기타 해석할 수 있는 모델 (0) | 2020.03.07 |
|---|---|
| [해석할 수 있는 기계학습(4-6)] 룰핏(RuleFit) (0) | 2020.03.01 |
| [해석할 수 있는 기계학습(4-4)] 의사결정 트리(Decision Tree) (1) | 2020.01.04 |
| [해석할 수 있는 기계학습(4-3)] GLM, GAM 및 상호작용 (3) | 2019.12.26 |
| [해석할 수 있는 기계학습(4-2)] 로지스틱 회귀 (0) | 2019.12.24 |




